Detailed Explanation and Implementation of GSO algorithm in Python
glowworm.py --- implementation of GSO
Glowworm Swarm Optimisation.pdf --- report on GSO
Glowworm Swarm.pptx --- Powerpoint presentation on GSO
Swarm robotics is an approach to the coordination of multirobot systems which consist of large numbers of mostly simple physical robots. It is supposed that a desired collective behavior emerges from the interactions between the robots and interactions of robots with the environment.
In applied mathematics, multimodal optimization deals with optimization tasks that involve finding all or most of the multiple (at least locally optimal) solutions of a problem, as opposed to a single best solution.
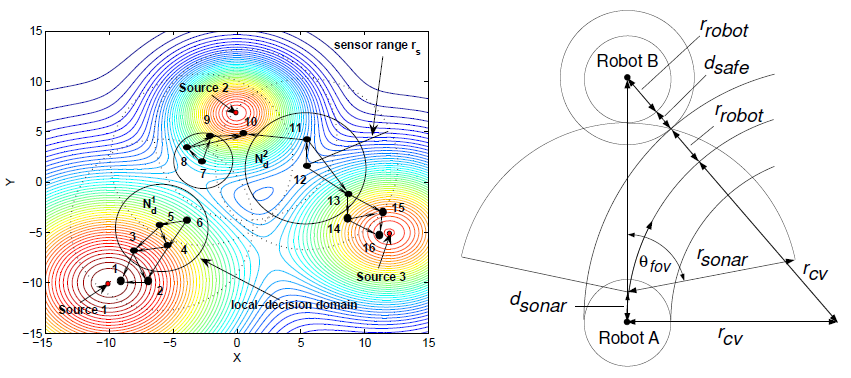
Glowworm swarm optimization (GSO) is a swarm intelligence based algorithm, introduced by K.N. Krishnanand and D. Ghose in 2005, for simultaneous computation of multiple optima of multimodal functions.The algorithm shares a few features with some better known algorithms, such as ant colony optimization and particle swarm optimization, but with several significant differences. The agents in GSO are thought of as glowworms that carry a luminescence quantity called luciferin along with them.
The glowworms encode the fitness of their current locations, evaluated using the objective function, into a luciferin value that they broadcast to their neighbors. The glowworm identifies its neighbors and computes its movements by exploiting an adaptive neighborhood, which is bounded above by its sensor range. Each glowworm selects, using a probabilistic mechanism, a neighbor that has a luciferin value higher than its own and moves toward it.
These movements—based only on local information and selective neighbor interactions—enable the swarm of glowworms to partition into disjoint subgroups that converge on multiple optima of a given multimodal function.
Unlike most other evolutionary multimodal optimization algorithms, the property of splitting into sub-groups allows the algorithm to simultaneously converge to local optima of different values, thus making it suitable for solving multiple signal source seeking problems using robots.