参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列:
- 序列中第一个单词是 beginWord 。
- 序列中最后一个单词是 endWord 。
- 每次转换只能改变一个字母。
- 转换过程中的中间单词必须是字典 wordList 中的单词。
- 给你两个单词 beginWord 和 endWord 和一个字典 wordList ,找到从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0。
示例 1:
- 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
- 输出:5
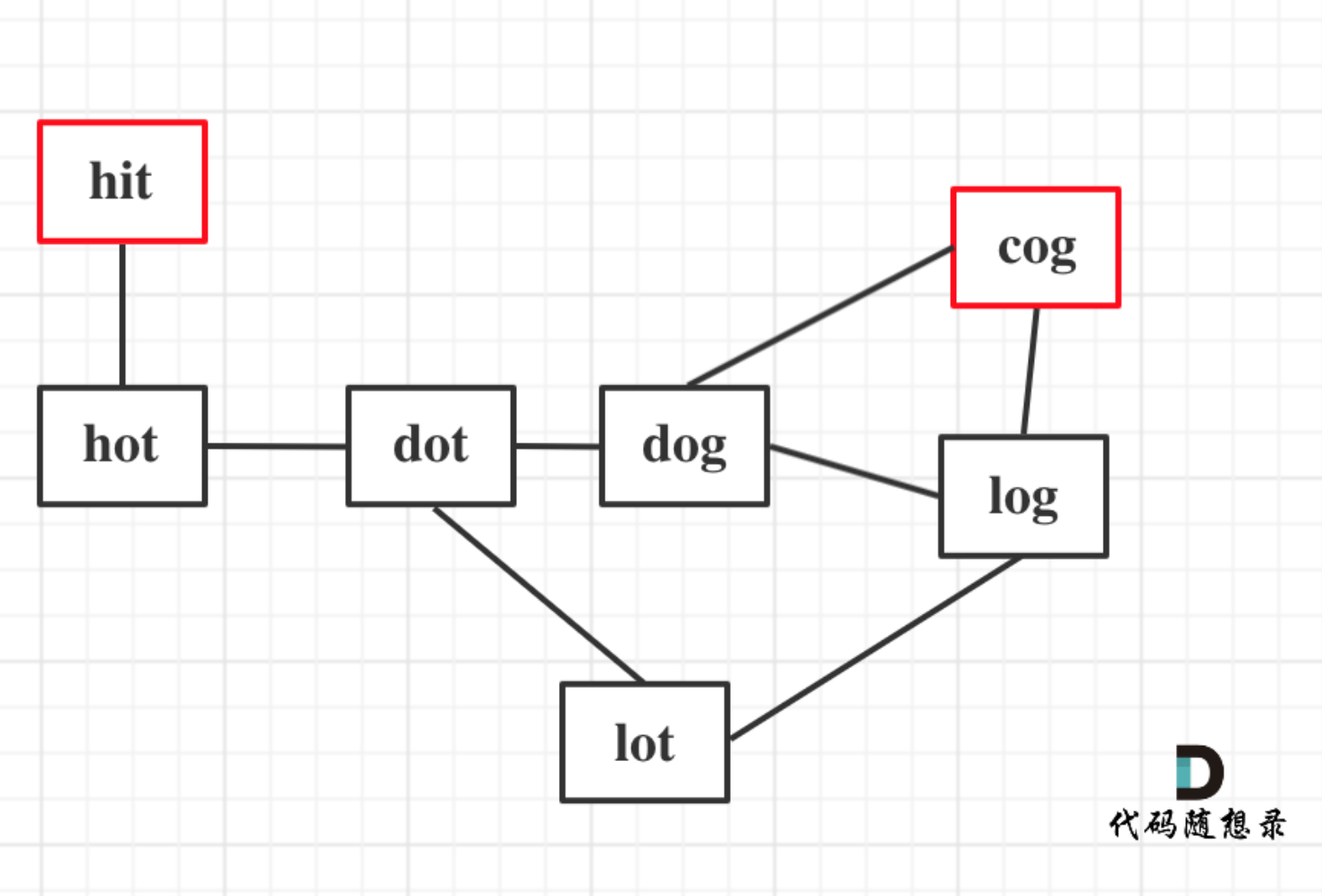
- 解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
示例 2:
- 输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
- 输出:0
- 解释:endWord "cog" 不在字典中,所以无法进行转换。
以示例1为例,从这个图中可以看出 hit 到 cog的路线,不止一条,有三条,两条是最短的长度为5,一条长度为6。
本题只需要求出最短长度就可以了,不用找出路径。
所以这道题要解决两个问题:
- 图中的线是如何连在一起的
- 起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个,所以判断点与点之间的关系,要自己判断是不是差一个字符,如果差一个字符,那就是有链接。
然后就是求起点和终点的最短路径长度,这里无向图求最短路,广搜最为合适,广搜只要搜到了终点,那么一定是最短的路径。因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜,会非常麻烦。
另外需要有一个注意点:
- 本题是一个无向图,需要用标记位,标记着节点是否走过,否则就会死循环!
- 本题给出集合是数组型的,可以转成set结构,查找更快一些
C++代码如下:(详细注释)
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
// 将vector转成unordered_set,提高查询速度
unordered_set<string> wordSet(wordList.begin(), wordList.end());
// 如果endWord没有在wordSet出现,直接返回0
if (wordSet.find(endWord) == wordSet.end()) return 0;
// 记录word是否访问过
unordered_map<string, int> visitMap; // <word, 查询到这个word路径长度>
// 初始化队列
queue<string> que;
que.push(beginWord);
// 初始化visitMap
visitMap.insert(pair<string, int>(beginWord, 1));
while(!que.empty()) {
string word = que.front();
que.pop();
int path = visitMap[word]; // 这个word的路径长度
for (int i = 0; i < word.size(); i++) {
string newWord = word; // 用一个新单词替换word,因为每次置换一个字母
for (int j = 0 ; j < 26; j++) {
newWord[i] = j + 'a';
if (newWord == endWord) return path + 1; // 找到了end,返回path+1
// wordSet出现了newWord,并且newWord没有被访问过
if (wordSet.find(newWord) != wordSet.end()
&& visitMap.find(newWord) == visitMap.end()) {
// 添加访问信息
visitMap.insert(pair<string, int>(newWord, path + 1));
que.push(newWord);
}
}
}
}
return 0;
}
};public int ladderLength(String beginWord, String endWord, List<String> wordList) {
HashSet<String> wordSet = new HashSet<>(wordList); //转换为hashset 加快速度
if (wordSet.size() == 0 || !wordSet.contains(endWord)) { //特殊情况判断
return 0;
}
Queue<String> queue = new LinkedList<>(); //bfs 队列
queue.offer(beginWord);
Map<String, Integer> map = new HashMap<>(); //记录单词对应路径长度
map.put(beginWord, 1);
while (!queue.isEmpty()) {
String word = queue.poll(); //取出队头单词
int path = map.get(word); //获取到该单词的路径长度
for (int i = 0; i < word.length(); i++) { //遍历单词的每个字符
char[] chars = word.toCharArray(); //将单词转换为char array,方便替换
for (char k = 'a'; k <= 'z'; k++) { //从'a' 到 'z' 遍历替换
chars[i] = k; //替换第i个字符
String newWord = String.valueOf(chars); //得到新的字符串
if (newWord.equals(endWord)) { //如果新的字符串值与endWord一致,返回当前长度+1
return path + 1;
}
if (wordSet.contains(newWord) && !map.containsKey(newWord)) { //如果新单词在set中,但是没有访问过
map.put(newWord, path + 1); //记录单词对应的路径长度
queue.offer(newWord);//加入队尾
}
}
}
}
return 0; //未找到
}var ladderLength = function(beginWord, endWord, wordList) {
// 将wordList转成Set,提高查询速度
const wordSet = new Set(wordList);
// Set元素个数为0 或者 endWord没有在wordSet出现,直接返回0
if (wordSet.size === 0 || !wordSet.has(endWord)) return 0;
// 记录word是否访问过
const visitMap = new Map();// <word, 查询到这个word路径长度>
// 初始化队列
const queue = [];
queue.push(beginWord);
// 初始化visitMap
visitMap.set(beginWord, 1);
while(queue.length !== 0){
let word = queue.shift(); // 删除队首元素,将它的值存放在word
let path = visitMap.get(word); // 这个word的路径长度
for(let i = 0; i < word.length; i++){ // 遍历单词的每个字符
for (let c = 97; c <= 122; c++) { // 对应26个字母ASCII值 从'a' 到 'z' 遍历替换
// 拼串得到新的字符串
let newWord = word.slice(0, i) + String.fromCharCode(c) + word.slice(i + 1);
if(newWord === endWord) return path + 1; // 找到了end,返回path+1
// wordSet出现了newWord,并且newWord没有被访问过
if(wordSet.has(newWord) && !visitMap.has(newWord)) {
// 添加访问信息
visitMap.set(newWord, path + 1);
queue.push(newWord);
}
}
}
}
return 0;
};