README_EN.md

654. Maximum Binary Tree

中文文档

Description

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

1. Create a root node whose value is the maximum value in nums.
2. Recursively build the left subtree on the subarray prefix to the left of the maximum value.
3. Recursively build the right subtree on the subarray suffix to the right of the maximum value.

Return the maximum binary tree built from nums.

 

Example 1:

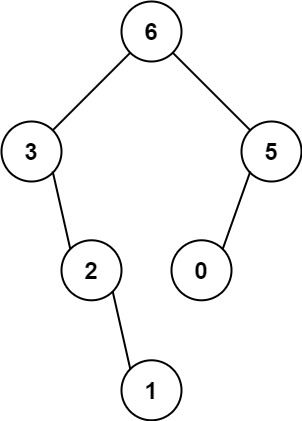
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
    - The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
        - Empty array, so no child.
        - The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
            - Empty array, so no child.
            - Only one element, so child is a node with value 1.
    - The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
        - Only one element, so child is a node with value 0.
        - Empty array, so no child.

Example 2:

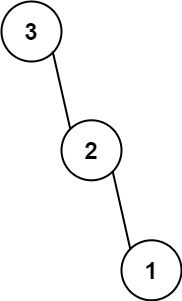
Input: nums = [3,2,1]
Output: [3,null,2,null,1]

 

Constraints:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• All integers in nums are unique.

Solutions

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:
        def inner(nums, l, r):
            if l > r:
                return None
            mx = l
            for i in range(l + 1, r + 1):
                if nums[mx] < nums[i]:
                    mx = i
            return TreeNode(nums[mx], inner(nums, l, mx - 1), inner(nums, mx + 1, r))

        return inner(nums, 0, len(nums) - 1)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums, 0, nums.length - 1);
    }

    private TreeNode construct(int[] nums, int l, int r) {
        if (l > r) {
            return null;
        }
        int mx = l;
        for (int i = l + 1; i <= r; ++i) {
            if (nums[mx] < nums[i]) {
                mx = i;
            }
        }
        return new TreeNode(nums[mx], construct(nums, l, mx - 1), construct(nums, mx + 1, r));
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return construct(nums, 0, nums.size() - 1);
    }

    TreeNode* construct(vector<int>& nums, int l, int r) {
        if (l > r) return nullptr;
        int mx = l;
        for (int i = l + 1; i <= r; ++i) {
            if (nums[mx] < nums[i]) mx = i;
        }
        TreeNode* root = new TreeNode(nums[mx]);
        root->left = construct(nums, l, mx - 1);
        root->right = construct(nums, mx + 1, r);
        return root;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func constructMaximumBinaryTree(nums []int) *TreeNode {
	return construct(nums, 0, len(nums)-1)
}

func construct(nums []int, l, r int) *TreeNode {
	if l > r {
		return nil
	}
	mx := l
	for i := l + 1; i <= r; i++ {
		if nums[mx] < nums[i] {
			mx = i
		}
	}
	return &TreeNode{
		Val:   nums[mx],
		Left:  construct(nums, l, mx-1),
		Right: construct(nums, mx+1, r),
	}
}

...