There are a total of n courses you have to take, labeled from 0 to n-1.
Some courses may have direct prerequisites, for example, to take course 0 you have first to take course 1, which is expressed as a pair: [1,0]
Given the total number of courses n, a list of direct prerequisite pairs and a list of queries pairs.
You should answer for each queries[i] whether the course queries[i][0] is a prerequisite of the course queries[i][1] or not.
Return a list of boolean, the answers to the given queries.
Please note that if course a is a prerequisite of course b and course b is a prerequisite of course c, then, course a is a prerequisite of course c.
Example 1:
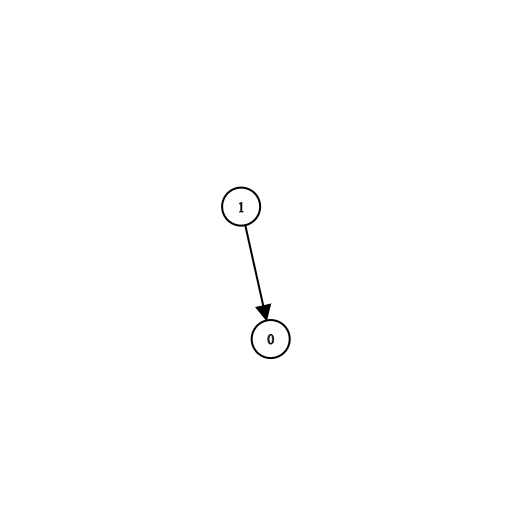
Input: n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] Output: [false,true] Explanation: course 0 is not a prerequisite of course 1 but the opposite is true.
Example 2:
Input: n = 2, prerequisites = [], queries = [[1,0],[0,1]] Output: [false,false] Explanation: There are no prerequisites and each course is independent.
Example 3:
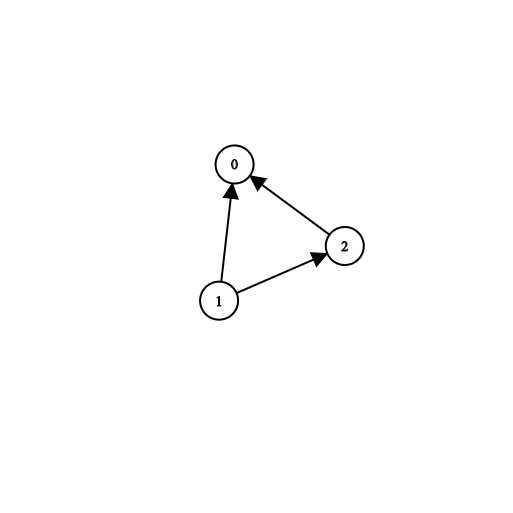
Input: n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] Output: [true,true]
Example 4:
Input: n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]] Output: [false,true]
Example 5:
Input: n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]] Output: [true,false,true,false]
Constraints:
2 <= n <= 1000 <= prerequisite.length <= (n * (n - 1) / 2)0 <= prerequisite[i][0], prerequisite[i][1] < nprerequisite[i][0] != prerequisite[i][1]- The prerequisites graph has no cycles.
- The prerequisites graph has no repeated edges.
1 <= queries.length <= 10^4queries[i][0] != queries[i][1]