FiBiNet.md

写在前面

FiBiNET(Feature Importance and Bilinear feature Interaction)是2019年发表在RecSys的一个模型，来自新浪微博张俊林老师的团队。这个模型如果从模型演化的角度来看， 主要是在特征重要性以及特征之间交互上做出了探索。所以，如果想掌握FiBiNet的话，需要掌握两大核心模块：

• 模型的特征重要性选择 --- SENET网络
• 特征之间的交互 --- 双线性交叉层(组合了内积和哈达玛积)

FiBiNet？ 我们先需要先了解这些

FiBiNet的提出动机是因为在特征交互这一方面， 目前的ctr模型要么是简单的两两embedding内积(这里针对离散特征)， 比如FM，FFM。 或者是两两embedding进行哈达玛积(NFM这种)， 作者认为这两种交互方式还是过于简单， 另外像NFM这种，FM这种，也忽视了特征之间的重要性程度。

对于特征重要性，作者在论文中举得例子非常形象

the feature occupation is more important than the feature hobby when we predict a person’s income

所以要想让模型学习到更多的信息， 从作者的角度来看，首先是离散特征之间的交互必不可少，且需要更细粒度。第二个就是需要考虑不同特征对于预测目标的重要性程度，给不同的特征根据重要性程度进行加权。 写到这里， 如果看过之前的文章的话，这个是不是和某些模型有些像呀， 没错，AFM其实考虑了这一点， 不过那里是用了一个Attention网络对特征进行的加权， 这里采用了另一种思路而已，即SENET， 所以这里我们如果是考虑特征重要性程度的话， 就有了两种思路：

• Attention
• SENET

而考虑特征交互的话， 思路应该会更多：

• PNN里面的内积和外积
• NFM里面的哈达玛积
• 这里的双线性函数交互(内积和哈达玛积的组合)

所以，读论文， 这些思路感觉要比模型本身重要，而读论文还有一个有意思的事情，那就是我们既能了解思路，也能想一下，为啥这些方法会有效果呢？ 我们自己能不能提出新的方法来呢？ 如果读一篇paper，再顺便把后面的这些问题想通了， 那么这篇paper对于我们来说就发挥效用了， 后面就可以用拉马努金式方法训练自己的思维。

在前面的准备工作中，作者依然是带着我们梳理了整个推荐模型的演化过程， 我们也简单梳理下，就当回忆:

• FNN: 下面是经过FM预训练的embedding层， 也就是先把FM训练好，得到各个特征的embedding，用这个embedding初始化FNN下面的embedding层， 上面是DNN。 这个模型用的不是很多，缺点是只能搞隐性高阶交互，并且下面的embedding和高层的DNN配合不是很好。
• WDL： 这是一个经典的W&D架构， w逻辑回归维持记忆， DNN保持高阶特征交互。问题是W端依然需要手动特征工程，也就是低阶交互需要手动来搞，需要一定的经验。一般工业上也不用了。
• DeepFM：对WDL的逻辑回归进行升级， 把逻辑回归换成FM， 这样能保证低阶特征的自动交互， 兼顾记忆和泛化性能，低阶和高阶交互。 目前这个模型在工业上非常常用，效果往往还不错，SOTA模型。
• DCN： 认为DeepFM的W端的FM的交互还不是很彻底，只能到二阶交互。所以就提出了一种交叉性网络，可以在W端完成高阶交互。
• xDeepFM: DCN的再次升级，认为DCN的wide端交叉网络这种element-wise的交互方式不行，且不是显性的高阶交互，所以提出了一个专门用户高阶显性交互的CIN网络， vector-wise层次上的特征交互。
• NFM: 下层是FM， 中间一个交叉池化层进行两两交互，然后上面接DNN， 工业上用的不多。
• AFM: 从NFM的基础上，考虑了交互完毕之后的特征重要性程度， 从NFM的基础上加了一个Attention网络，所以如果用的话，也应该用AFM。

综上， 这几个网络里面最常用的还是属DeepFM了， 当然对于交互来讲，在我的任务上试过AFM和xDeepFM， 结果是AFM和DeepFM差不多持平， 而xDeepFM要比这俩好一些，但并不多，而考虑完了复杂性， 还是DeepFM或者AFM。

对于上面模型的问题，作者说了两点，第一个是大部分模型没有考虑特征重要性，也就是交互完事之后，没考虑对于预测目标来讲谁更重要，一视同仁。 第二个是目前的两两特征交互，大部分依然是内积或者哈达玛积， 作者认为还不是细粒度(fine-grained way)交互。

那么，作者是怎么针对这两个问题进行改进的呢？ 为什么这么改进呢？

FiBiNet模型的理论以及论文细节

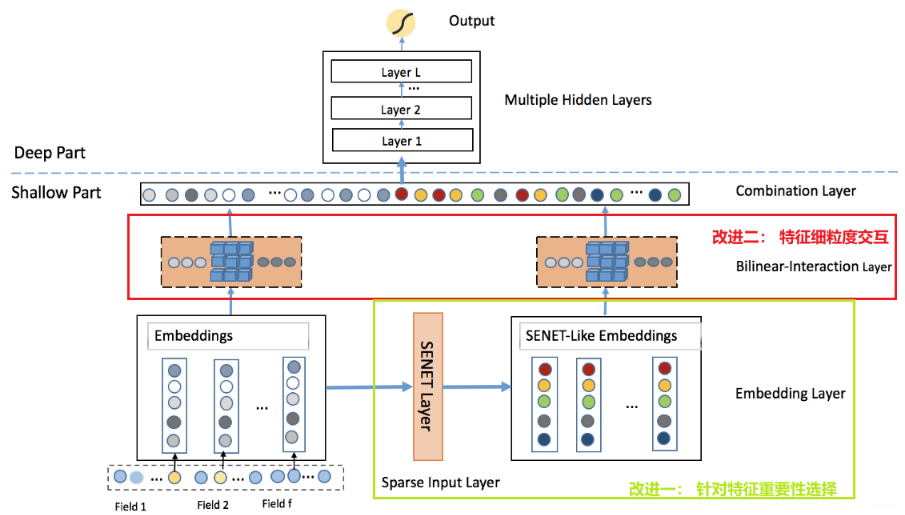
这里我们直接分析模型架构即可， 因为这个模型不是很复杂，也非常好理解前向传播的过程：

从模型架构上来看，如果把我框出来的两部分去掉， 这个基本上就退化成了最简单的推荐深度模型DeepCrossing，甚至还比不上那个(那个还用了残差网络)。不过，加上了两个框，效果可就不一样了。所以下面重点是剖析下这两个框的结构，其他的简单一过即可。

梳理细节之前， 先说下前向传播的过程。
首先，我们输入的特征有离散和连续，对于连续的特征，输入完了之后，先不用管，等待后面拼起来进DNN即可，这里也没有刻意处理连续特征。
对于离散特征，过embedding转成低维稠密，一般模型的话，这样完了之后，就去考虑embedding之间交互了。 而这个模型不是， 在得到离散特征的embedding之后，分成了两路

• 一路保持原样， 继续往后做两两之间embedding交互，不过这里的交互方式，不是简单的内积或者哈达玛积，而是采用了非线性函数，这个后面会提到。
• 另一路，过一个SENET Layer， 过完了之后得到的输出是和原来embedding有着相同维度的，这个SENET的理解方式和Attention网络差不多，也是根据embedding的重要性不同出来个权重乘到了上面。 这样得到了SENET-like Embedding，就是加权之后的embedding。 这时候再往上两两双线性交互。

两路embedding都两两交互完事， Flatten展平，和连续特征拼在一块过DNN输出。

Embedding Layer

这个不多讲， 整理这个是为了后面统一符号。

假设我们有$f$个离散特征，经过embedding层之后，会得到$E=\left[e_{1}, e_{2}, \cdots, e_{i}, \cdots, e_{f}\right]$， 其中$e_{i} \in R^{k}$，表示第$i$个离散特征对应的embedding向量，$k$维。

SENET Layer

这是第一个重点，首先这个网络接收的输入是上面的$E=\left[e_{1}, e_{2}, \cdots, e_{i}, \cdots, e_{f}\right]$， 网络的输出也是个同样大小的张量(None, f, k)矩阵。 结构如下：

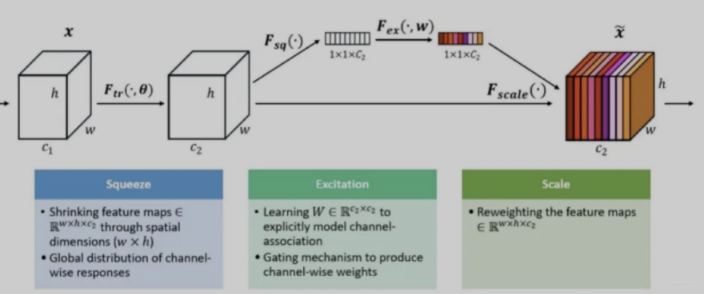
SENet由自动驾驶公司Momenta在2017年提出，在当时，是一种应用于图像处理的新型网络结构。它基于CNN结构，通过对特征通道间的相关性进行建模，对重要特征进行强化来提升模型准确率，本质上就是针对CNN中间层卷积核特征的Attention操作。ENet仍然是效果最好的图像处理网络结构之一。

SENet能否用到推荐系统？--- 张俊林老师的知乎(链接在文末)
推荐领域里面的特征有个特点，就是海量稀疏，意思是大量长尾特征是低频的，而这些低频特征，去学一个靠谱的Embedding是基本没希望的，但是你又不能把低频的特征全抛掉，因为有一些又是有效的。既然这样，如果我们把SENet用在特征Embedding上，类似于做了个对特征的Attention，弱化那些不靠谱低频特征Embedding的负面影响，强化靠谱低频特征以及重要中高频特征的作用，从道理上是讲得通的

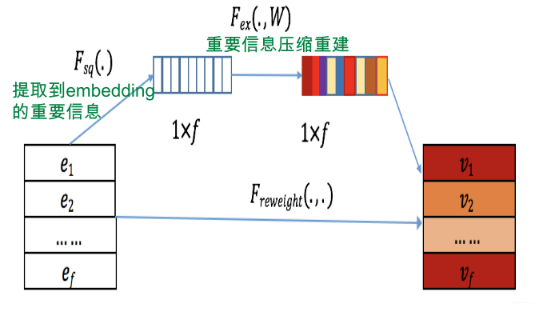
所以拿来用了再说， 把SENet放在Embedding层之上，通过SENet网络，动态地学习这些特征的重要性。对于每个特征学会一个特征权重，然后再把学习到的权重乘到对应特征的Embedding里，这样就可以动态学习特征权重，通过小权重抑制噪音或者无效低频特征，通过大权重放大重要特征影响的目的。在推荐系统里面， 结构长这个样子：

下面看下这个网络里面的具体计算过程， SENET主要分为三个步骤Squeeze, Excitation, Re-weight。

• 在Squeeze阶段，我们对每个特征的Embedding向量进行数据压缩与信息汇总，如下：

  $$ z_{i}=F_{s q}\left(e_{i}\right)=\frac{1}{k} \sum_{t=1}^{k} e_{i}^{(t)} $$

  假设某个特征$v_i$是$k$维大小的$Embedding$，那么我们对$Embedding$里包含的$k$维数字求均值，得到能够代表这个特征汇总信息的数值 $z_i$，也就是说，把第$i$个特征的$Embedding$里的信息压缩到一个数值。原始版本的SENet，在这一步是对CNN的二维卷积核进行$Max$操作的，这里等于对某个特征Embedding元素求均值。我们试过，在推荐领域均值效果比$Max$效果好，这也很好理解，因为图像领域对卷积核元素求$Max$，等于找到最强的那个特征，而推荐领域的特征$Embedding$，每一位的数字都是有意义的，所以求均值能更好地保留和融合信息。通过Squeeze阶段，对于每个特征$v_i$ ，都压缩成了单个数值$z_i$，假设特征Embedding层有$f$个特征，就形成Squeeze向量$Z$，向量大小$f$。

• Excitation阶段，这个阶段引入了中间层比较窄的两层MLP网络，作用在Squeeze阶段的输出向量$Z$上，如下：

  $$ A=F_{e x}(Z)=\sigma_{2}\left(W_{2} \sigma_{1}\left(W_{1} Z\right)\right) $$

  $\sigma$非线性激活函数，一般$relu$。本质上，这是在做特征的交叉，也就是说，每个特征以一个$Bit$来表征，通过MLP来进行交互，通过交互，得出这么个结果：对于当前所有输入的特征，通过相互发生关联，来动态地判断哪些特征重要，哪些特征不重要。

  其中，第一个MLP的作用是做特征交叉，第二个MLP的作用是为了保持输出的大小维度。因为假设Embedding层有$f$个特征，那么我们需要保证输出$f$个权重值，而第二个MLP就是起到将大小映射到$f$个数值大小的作用。
  
  这样，经过两层MLP映射，就会产生$f$个权重数值，第$i$个数值对应第$i$个特征Embedding的权重$a_i$ 。
  
  这个东西有没有感觉和自动编码器很像，虽然不是一样的作用， 但网络结构是一样的。这就是知识串联的功效哈哈。

  

  瞬间是不是就把SENet这里的网络结构记住了哈哈。下面再分析下维度， SENet的输入是$E$，这个是(None, f, k)的维度， 通过Squeeze阶段，得到了(None, f)的矩阵，这个也就相当于Layer L1的输入(当然这里没有下面的偏置哈)，接下来过MLP1， 这里的$W_{1} \in R^{f \times \frac{f}{r}}, W_{2} \in R^{\frac{f}{r} \times f}$, 这里的$r$叫做reduction ratio， $\frac{f}{r}$这个就是中间层神经元的个数， $r$表示了压缩的程度。

• Re-Weight 我们把Excitation阶段得到的每个特征对应的权重$a_i$，再乘回到特征对应的Embedding里，就完成了对特征重要性的加权操作。 $$V=F_{\text {ReWeight }}(A, E)=\left[a_{1} \cdot e_{1}, \cdots, a_{f} \cdot e_{f}\right]=\left[v_{1}, \cdots, v_{f}\right]$$ $a_{i} \in R, e_{i} \in R^{k}$, and $v_{i} \in R^{k}$。$a_i$数值大，说明SENet判断这个特征在当前输入组合里比较重要， $a_i$数值小，说明SENet判断这个特征在当前输入组合里没啥用。如果非线性函数用Relu，会发现大量特征的权重会被Relu搞成0，也就是说，其实很多特征是没啥用的。

这样，就可以将SENet引入推荐系统，用来对特征重要性进行动态判断。注意，所谓动态，指的是比如对于某个特征，在某个输入组合里可能是没用的，但是换一个输入组合，很可能是重要特征。它重要不重要，不是静态的，而是要根据当前输入，动态变化的。

这里正确的理解，算是一种特征重要性选择的思路， SENET和AFM的Attention网络是起着同样功效的一个网络。只不过那个是在特征交互之后进行特征交互重要性的选择，而这里是从embedding这里先压缩，再交互，再选择，去掉不太重要的特征。 考虑特征重要性上的两种考虑思路，难以说孰好孰坏，具体看应用场景。 不过如果分析下这个东西为啥会有效果， 就像张俊林老师提到的那样， 在Excitation阶段， 各个特征过了一个MLP进行了特征组合， 这样就真有可能过滤掉对于当前的交互不太重要的特征。 至于是不是， 那神经网络这东西就玄学了，让网络自己去学吧。

Bilinear-Interaction Layer

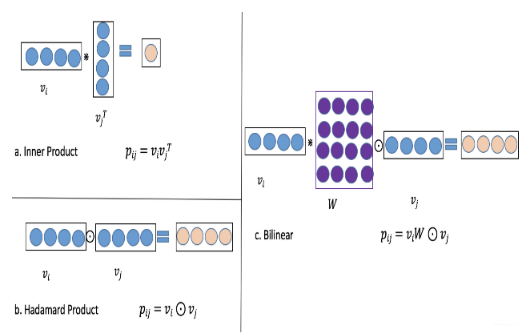
特征重要性选择完事， 接下来就是研究特征交互， 这里作者直接就列出了目前的两种常用交互以及双线性交互:

这个图其实非常了然了。以往模型用的交互， 内积的方式(FM,FFM)这种或者哈达玛积的方式(NFM,AFM)这种。

所谓的双线性，其实就是组合了内积和哈达玛积的操作，看上面的右图。就是在$v_i$和$v_j$之间先加一个$W$矩阵， 这个$W$矩阵的维度是$(f,f)$, $v_i, v_j$是$(1,f)$的向量。 先让$v_i$与$W$内积，得到$(1,f)$的向量，这时候先仔细体会下这个新向量的每个元素，相当于是原来向量$v_i$在每个维度上的线性组合了。这时候再与$v_j$进行哈达玛积得到结果。

这里我不由自主的考虑了下双线性的功效，也就是为啥作者会说双线性是细粒度，下面是我自己的看法哈。

• 如果我们单独先看内积操作，特征交互如果是两个向量直接内积，这时候， 结果大的，说明两个向量相似或者特征相似， 但向量内积，其实是相当于向量的各个维度先对应位置元素相乘再相加求和。 这个过程中认为的是向量的各个维度信息的重要性是一致的。类似于$v_1+v_2+..v_k$， 但真的一致吗？ --- 内积操作没有考虑向量各个维度的重要性
• 如果我们单独看哈达玛积操作， 特征交互如果是两个向量哈达玛积，这时候，是各个维度对应位置元素相乘得到一个向量， 而这个向量往往后面会进行线性或者非线性交叉的操作， 最后可能也会得到具体某个数值，但是这里经过了线性或者非线性交叉操作之后， 有没有感觉把向量各个维度信息的重要性考虑了进来？ 就类似于$w_1v_{i1j1}+w_2k_{v2j2},...w_kv_{vkjk}$。 如果模型认为重要性相同，那么哈达玛积还有希望退化成内积，所以哈达玛积感觉考虑的比内积就多了一些。 --- 哈达玛积操作自身也没有考虑各个维度重要性，但通过后面的线性或者非线性操作，有一定的维度重要性在里面
• 再看看这个双线性， 是先内积再哈达玛积。这个内积操作不是直接$v_i$和$v_j$内积，而是中间引入了个$W$矩阵，参数可学习。 那么$v_i$和$W$做内积之后，虽然得到了同样大小的向量，但是这个向量是$v_i$各个维度元素的线性组合，相当于$v_i$变成了$[w_{11}v_{i1}+...w_{1k}v_{ik}, w_{21}v_{i1}+..w_{2k}v_{ik}, ...., w_{k1}v_{i1}+...w_{kk}v_{ik}]$， 这时候再与$v_j$哈达玛积的功效，就变成了$[(w_{11}v_{i1}+...w_{1k}v_{ik})v_{j1}, (w_{21}v_{i1}+..w_{2k}v_{ik})v_{j2}, ...., (w_{k1}v_{i1}+...w_{kk}v_{ik})v_{j_k}]$， 这时候，就可以看到，如果这里的$W$是个对角矩阵，那么这里就退化成了哈达玛积。 所以双线性感觉考虑的又比哈达玛积多了一些。如果后面再走一个非线性操作的话，就会发现这里同时考虑了两个交互向量各个维度上的重要性。---双线性操作同时可以考虑交互的向量各自的各个维度上的重要性信息， 这应该是作者所说的细粒度，各个维度上的重要性

当然思路是思路，双线性并不一定见得一定比哈达玛积有效， SENET也不一定就会比原始embedding要好，一定要辩证看问题

这里还有个厉害的地方在于这里的W有三种选择方式，也就是三种类型的双线性交互方式。

1. Field-All Type $$ p_{i j}=v_{i} \cdot W \odot v_{j} $$ 也就是所有的特征embedding共用一个$W$矩阵，这也是Field-All的名字来源。$W \in R^{k \times k}, \text { and } v_{i}, v_{j} \in R^{k}$。这种方式最简单
2. Field-Each Type $$ p_{i j}=v_{i} \cdot W_{i} \odot v_{j} $$ 每个特征embedding共用一个$W$矩阵， 那么如果有$f$个特征的话，这里的$W_i$需要$f$个。所以这里的参数个数$f-1\times k\times k$， 这里的$f-1$是因为两两组合之后，比如[0,1,2]， 两两组合[0,1], [0,2], [1,2]。 这里用到的域是0和1。
3. Field-Interaction Type $$ p_{i j}=v_{i} \cdot W_{i j} \odot v_{j} $$ 每组特征交互的时候，用一个$W$矩阵， 那么这里如果有$f$个特征的话，需要$W_{ij}$是$\frac{f(f-1)}{2}$个。参数个数$\frac{f(f-1)}{2}\times k\times k$个。

不知道看到这里，这种操作有没有种似曾相识的感觉， 有没有想起FM和FFM， 反正我是不自觉的想起了哈哈，不知道为啥。总感觉FM的风格和上面的Field-All很像， 而FFM和下面的Field-Interaction很像。

我们的原始embedding和SKNET-like embedding都需要过这个层，那么得到的就是一个双线性两两组合的矩阵， 维度是$(\frac{f(f-1)}{2}, k)$的矩阵。

Combination Layer

这个层的作用就是把目前得到的特征拼起来 $$ c=F_{\text {concat }}(p, q)=\left[p_{1}, \cdots, p_{n}, q_{1}, \cdots, q_{n}\right]=\left[c_{1}, \cdots, c_{2 n}\right] $$ 这里他直拼了上面得到的两个离散特征通过各种交互之后的形式，如果是还有连续特征的话，也可以在这里拼起来，然后过DNN，不过这里其实还省略了一步操作就是Flatten，先展平再拼接。

DNN和输出层

这里就不多说了， DNN的话普通的全连接网络， 再捕捉一波高阶的隐性交互。 $$ a^{(l)}=\sigma\left(W^{(l)} a^{(l-1)}+b^{(l)}\right) $$ 而输出层 $$ \hat{y}=\sigma\left(w_{0}+\sum_{i=0}^{m} w_{i} x_{i}+y_{d}\right) $$ 分类问题损失函数： $$ \operatorname{loss}=-\frac{1}{N} \sum_{i=1}^{N}\left(y_{i} \log \left(\hat{y}{i}\right)+\left(1-y{i}\right) * \log \left(1-\hat{y}_{i}\right)\right) $$ 这里就不解释了。

其他重要细节

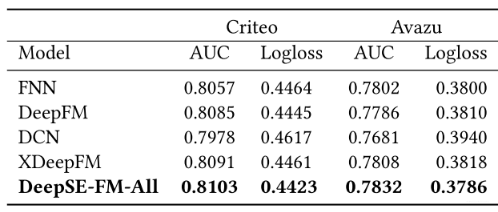
实验部分，这里作者也是做了大量的实验来证明提出的模型比其他模型要好，这个就不说了。

竟然比xDeepFM都要好。

在模型评估指标上，用了AUC和Logloss，这个也是常用的指标，Logloss就是交叉熵损失， 反映了样本的平均偏差，经常作为模型的损失函数来做优化，可是，当训练数据正负样本不平衡时，比如我们经常会遇到正样本很少，负样本很多的情况，此时LogLoss会倾向于偏向负样本一方。 而AUC评估不会受很大影响，具体和AUC的计算原理有关。这个在这里就不解释了。

其次了解到的一个事情：

接下来，得整理下双线性与哈达玛积的组合类型，因为我们这个地方其实有两路embedding的， 一路是原始embedding， 一路是SKNet侧的embedding。而面临的组合方式，有双线性和哈达玛积两种。那么怎么组合会比较好呢？ 作者做了实验。结论是，作者建议:

深度学习模型中，原始那边依然哈达玛，SE那边双线性， 可能更有效， 不过后面的代码实现里面，都用了双线性。

而具体，在双线性里面，那种W的原则有效呢？ 这个视具体的数据集而定。

超参数选择，主要是embedding维度以及DNN层数， embedding维度这个10-50， 不同的数据集可能表现不一样， 但尽量不要超过50了。否则在DNN之前的特征维度会很大。

DNN层数，作者这里建议3层，而每一层神经单元个数，也是没有定数了。

这里竟然没有说$r$的确定范围。 Deepctr里面默认是3。

对于实际应用的一些经验:

1. SE-FM 在实验数据效果略高于 FFM，优于FM，对于模型处于低阶的团队，升级FM、SE-FM成本比较低

2. deepSE-FM 效果优于DCN、XDeepFM 这类模型，相当于XDeepFM这种难上线的模型来说，很值得尝试，不过大概率怀疑是增加特征交叉的效果，特征改进比模型改进work起来更稳

3. 实验中增加embeding 长度费力不讨好，效果增加不明显，如果只是增加长度不改变玩法边际效应递减，不增加长度增加emmbedding 交叉方式类似模型的ensemble更容易有效果

FiBiNet模型的代码复现及重要结构解释

这里的话，参考deepctr修改的简化版本。

全貌

对于输入，就不详细的说了，在xDeepFM那里已经解释了， 首先网络的整体全貌:

def fibinet(linear_feature_columns, dnn_feature_columns,  bilinear_type='interaction', reduction_ratio=3, hidden_units=[128, 128]):
    """
    :param linear_feature_columns, dnn_feature_columns: 封装好的wide端和deep端的特征
    :param bilinear_type: 双线性交互类型， 有'all', 'each', 'interaction'三种
    :param reduction_ratio: senet里面reduction ratio
    :param hidden_units: DNN隐藏单元个数
    """
    
    # 构建输出层, 即所有特征对应的Input()层， 用字典的形式返回，方便后续构建模型
    dense_input_dict, sparse_input_dict = build_input_layers(linear_feature_columns + dnn_feature_columns)
    
    # 构建模型的输入层，模型的输入层不能是字典的形式，应该将字典的形式转换成列表的形式
    # 注意：这里实际的输入预Input层对应，是通过模型输入时候的字典数据的key与对应name的Input层
    input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())
    
    # 线性部分的计算逻辑 -- linear
    linear_logits = get_linear_logits(dense_input_dict, sparse_input_dict, linear_feature_columns)
    
    # 构建维度为k的embedding层，这里使用字典的形式返回，方便后面搭建模型
    # 线性层和dnn层统一的embedding层
    embedding_layer_dict = build_embedding_layers(linear_feature_columns+dnn_feature_columns, sparse_input_dict, is_linear=False)
    
    # DNN侧的计算逻辑 -- Deep
    # 将dnn_feature_columns里面的连续特征筛选出来，并把相应的Input层拼接到一块
    dnn_dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), dnn_feature_columns)) if dnn_feature_columns else []
    dnn_dense_feature_columns = [fc.name for fc in dnn_dense_feature_columns]
    dnn_concat_dense_inputs = Concatenate(axis=1)([dense_input_dict[col] for col in dnn_dense_feature_columns])
    
    # 将dnn_feature_columns里面的离散特征筛选出来，相应的embedding层拼接到一块,然后过SENet_layer
    dnn_sparse_kd_embed = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=False)
    sparse_embedding_list = Concatenate(axis=1)(dnn_sparse_kd_embed)
    
    # SENet layer
    senet_embedding_list = SENETLayer(reduction_ratio)(sparse_embedding_list)
    
    # 双线性交互层
    senet_bilinear_out = BilinearInteraction(bilinear_type=bilinear_type)(senet_embedding_list)
    raw_bilinear_out = BilinearInteraction(bilinear_type=bilinear_type)(sparse_embedding_list)
    
    bilinear_out = Flatten()(Concatenate(axis=1)([senet_bilinear_out, raw_bilinear_out]))
    
    # DNN层的输入和输出
    dnn_input = Concatenate(axis=1)([bilinear_out, dnn_concat_dense_inputs])
    dnn_out = get_dnn_output(dnn_input, hidden_units=hidden_units)
    dnn_logits = Dense(1)(dnn_out)
                             
    # 最后的输出
    final_logits = Add()([linear_logits, dnn_logits])
    
    # 输出层
    output_layer = Dense(1, activation='sigmoid')(final_logits)
    
    model = Model(input_layers, output_layer)
    
    return model

这里依然是是采用了线性层计算与DNN相结合的方式。 前向传播这里也不详细描述了。这里面重点是SENETLayer和BilinearInteraction层，其他的和之前网络模块基本上一样。

SENETLayer

这里的输入是[None, field_num embed_dim]的维度，也就是离散特征的embedding， 拿到这个输入之后，三个步骤，得到的是一个[None, feild_num, embed_dim]的同样维度的矩阵，只不过这里是SKNET-like embedding了。

class SENETLayer(Layer):
    def __init__(self, reduction_ratio, seed=2021):
        super(SENETLayer, self).__init__()
        self.reduction_ratio = reduction_ratio
        self.seed = seed
    
    def build(self, input_shape):
        # input_shape  [None, field_nums, embedding_dim]
        self.field_size = input_shape[1]
        self.embedding_size = input_shape[-1]
        
        # 中间层的神经单元个数 f/r
        reduction_size = max(1, self.field_size // self.reduction_ratio)
        
        # FC layer1和layer2的参数
        self.W_1 = self.add_weight(shape=(
            self.field_size, reduction_size), initializer=glorot_normal(seed=self.seed), name="W_1")
        self.W_2 = self.add_weight(shape=(
            reduction_size, self.field_size), initializer=glorot_normal(seed=self.seed), name="W_2")

        self.tensordot = tf.keras.layers.Lambda(
            lambda x: tf.tensordot(x[0], x[1], axes=(-1, 0)))

        # Be sure to call this somewhere!
        super(SENETLayer, self).build(input_shape)
    
    def call(self, inputs):
        # inputs [None, field_num, embed_dim]
        
        # Squeeze -> [None, field_num]
        Z = tf.reduce_mean(inputs, axis=-1)
        
        # Excitation
        A_1 = tf.nn.relu(self.tensordot([Z, self.W_1]))   # [None, reduction_size]
        A_2 = tf.nn.relu(self.tensordot([A_1, self.W_2]))   # [None, field_num]
        
        # Re-Weight
        V = tf.multiply(inputs, tf.expand_dims(A_2, axis=2))  # [None, field_num, embedding_dim]

        return V

三个步骤还是比较好理解的， 这里这种自定义层权重的方式需要学习下。

4.3 BilinearInteraction Layer

这里接收的输入同样是[None, field_num embed_dim]的维度离散特征的embedding。 输出是来两两交互完毕的矩阵$[None, \frac{f(f-1)}{2}, embed_dim]$

这里的双线性交互有三种形式，具体实现的话可以参考下面的代码，我加了注释， 后面两种用到了组合的方式， 感觉人家这种实现方式还是非常巧妙的。

class BilinearInteraction(Layer):
    """BilinearInteraction Layer used in FiBiNET.
      Input shape
        - 3D tensor with shape: ``(batch_size,field_size,embedding_size)``.
      Output shape
        - 3D tensor with shape: ``(batch_size,filed_size*(filed_size-1)/2,embedding_size)``.
    """
    def __init__(self, bilinear_type="interaction", seed=2021, **kwargs):
        super(BilinearInteraction, self).__init__(**kwargs)
        self.bilinear_type = bilinear_type
        self.seed = seed
    
    def build(self, input_shape):
        # input_shape: [None, field_num, embed_num]
        self.field_size = input_shape[1]
        self.embedding_size = input_shape[-1]
        
        if self.bilinear_type == "all":   # 所有embedding矩阵共用一个矩阵W
            self.W = self.add_weight(shape=(self.embedding_size, self.embedding_size), initializer=glorot_normal(
                seed=self.seed), name="bilinear_weight")
        elif self.bilinear_type == "each": # 每个field共用一个矩阵W
            self.W_list = [self.add_weight(shape=(self.embedding_size, self.embedding_size), initializer=glorot_normal(
                seed=self.seed), name="bilinear_weight" + str(i)) for i in range(self.field_size-1)]
        elif self.bilinear_type == "interaction":  # 每个交互用一个矩阵W
            self.W_list = [self.add_weight(shape=(self.embedding_size, self.embedding_size), initializer=glorot_normal(
                seed=self.seed), name="bilinear_weight" + str(i) + '_' + str(j)) for i, j in
                           itertools.combinations(range(self.field_size), 2)]
        else:
            raise NotImplementedError

        super(BilinearInteraction, self).build(input_shape)  # Be sure to call this somewhere!

    def call(self, inputs):
        # inputs: [None, field_nums, embed_dims]
        # 这里把inputs从field_nums处split, 划分成field_nums个embed_dims长向量的列表
        inputs = tf.split(inputs, self.field_size, axis=1)  # [(None, embed_dims), (None, embed_dims), ..] 
        n = len(inputs)  # field_nums个
        
        if self.bilinear_type == "all":
            # inputs[i] (none, embed_dims)    self.W (embed_dims, embed_dims) -> (None, embed_dims)
            vidots = [tf.tensordot(inputs[i], self.W, axes=(-1, 0)) for i in range(n)]   # 点积
            p = [tf.multiply(vidots[i], inputs[j]) for i, j in itertools.combinations(range(n), 2)]  # 哈达玛积
        elif self.bilinear_type == "each":
            vidots = [tf.tensordot(inputs[i], self.W_list[i], axes=(-1, 0)) for i in range(n - 1)]
            # 假设3个域， 则两两组合[(0,1), (0,2), (1,2)]  这里的vidots是第一个维度， inputs是第二个维度 哈达玛积运算
            p = [tf.multiply(vidots[i], inputs[j]) for i, j in itertools.combinations(range(n), 2)]
        elif self.bilinear_type == "interaction":
            # combinations(inputs, 2)  这个得到的是两两向量交互的结果列表
            # 比如 combinations([[1,2], [3,4], [5,6]], 2)
            # 得到 [([1, 2], [3, 4]), ([1, 2], [5, 6]), ([3, 4], [5, 6])]  (v[0], v[1]) 先v[0]与W点积，然后再和v[1]哈达玛积
            p = [tf.multiply(tf.tensordot(v[0], w, axes=(-1, 0)), v[1])
                 for v, w in zip(itertools.combinations(inputs, 2), self.W_list)]
        else:
            raise NotImplementedError
            
        output = Concatenate(axis=1)(p)
        return output

这里第一个是需要学习组合交互的具体实现方式， 人家的代码方式非常巧妙，第二个会是理解下。

关于FiBiNet网络的代码细节就到这里了，具体代码放到了我的GitHub链接上了。

总结

这篇文章主要是整理了一个新模型， 这个模型是在特征重要性选择以及特征交互上做出了新的探索，给了我们两个新思路。 这里面还有两个重要的地方，感觉是作者对于SENET在推荐系统上的使用思考，也就是为啥能把这个东西迁过来，以及为啥双线性会更加细粒度，这种双线性函数的优势在哪儿？我们通常所说的知其然，意思是针对特征交互， 针对特征选择，我又有了两种考虑思路双线性和SENet， 而知其所以然，应该考虑为啥双线性或者SENET会有效呢？ 当然在文章中给出了自己的看法，当然这个可能不对哈，是自己对于问题的一种思考， 欢迎伙伴们一块讨论。

我现在读论文，一般读完了之后，会刻意逼着自己想这么几个问题：

本篇论文核心是讲了个啥东西？ 是为啥会提出这么个东西？ 为啥这个新东西会有效？ 与这个新东西类似的东西还有啥？ 在工业上通常会怎么用？

一般经过这样的灵魂5问就能把整篇论文拎起来了，而读完了这篇文章，你能根据这5问给出相应的答案吗？ 欢迎在下方留言呀。

还有一种读论文的厉害姿势，和张俊林老师学的，就是拉马努金式思维，就是读论文之前，看完题目之后， 不要看正文，先猜测作者在尝试解决什么样的问题，比如

看到特征重要性和双线性特征交互， 就大体上能猜测到这篇推荐论文讲的应该是和特征选择和特征交互相关的知识。 那么如果是我解决这两方面的话应该怎么解决呢？

• 特征选择 --- 联想到Attention
• 特征交互 --- 联想到哈达玛积或者内积

这时候， 就可以读论文了，读完之后， 对比下人家提出的想法和自己的想法的区别，考虑下为啥会有这样的区别？ 然后再就是上面的灵魂5问， 通过这样的方式读论文， 能够理解的更加深刻，就不会再有读完很多论文，依然很虚的感觉，啥也没记住了。 如果再能花点时间总结输出下， 和之前的论文做一个对比串联，再花点时间看看代码，复现下，用到自己的任务上。 那么这样， 就算是真正把握住模型背后的思想了，而不是仅仅会个模型而已， 并且这种读论文方式，只要习惯了之后， 读论文会很快，因为我隐约发现，万变不离其宗， 论文里面抛去实验部分，抛去前言部分， 剩下的精华其实没有几页的。当然整理会花费时间， 但也有相应的价值在里面。 我以后整理，也是以经典思路模型为主， 对于一般的，我会放到论文总结的专栏里面，一下子两三篇的那种整理，只整理大体思路就即可啦。

下面只整理来自工业大佬的使用经验和反思， 具体参考下面的第二篇参考:

• 适用的数据集 虽然模型是针对点击率预测的场景提出的，但可以尝试的数据场景也不少，比较适合包含大量categorical feature且这些feature cardinality本身很高，或者因为encode method导致的某些feature维度很高且稀疏的情况。推荐系统的场景因为大量的user/item属性都是符合这些要求的，所以效果格外好，但我们也可以举一反三把它推广到其他相似场景。另外，文字描述类的特征（比如人工标注的主观评价，名字，地址信息……）可以用tokenizer处理成int sequence/matrix作为embedding feature喂进模型，丰富的interaction方法可以很好的学习到这些样本中这些特征的相似之处并挖掘出一些潜在的关系。

• 回归和分类问题都可以做，无非改一下DNN最后一层的activation函数和objective，没有太大的差别。

• 如果dense feature比较多而且是分布存在很多异常值的numeric feature，尽量就不要用FiBiNET了，相比大部分NN没有优势不说，SENET那里的一个最大池化极其容易把特征权重带偏，如果一定要上，可能需要修改一下池化的方法。

• DeepCTR的实现还把指定的linear feature作为类似于WDL中的wide部分直接输入到DNN的最后一层，以及DNN部分也吸收了一部分指定的dnn feature中的dense feature直接作为输入。毫无疑问，DeepCTR作者在尽可能的保留更多的特征作为输入防止信息的丢失。

• 使用Field-Each方式能够达到最好的预测准确率，而且相比默认的Field-Interaction，参数也减少了不少，训练效率更高。当然，三种方式在准确率方面差异不是非常巨大。

• reduce ratio设置到8效果最好，这方面我的经验和不少人达成了共识，SENET用于其他学习任务也可以得到相似的结论。 -- 这个试了下，确实有效果

• 使用dropout方法扔掉hidden layer里的部分unit效果会更好，系数大约在0.3时最好，原文用的是0.5,请根据具体使用的网络结构和数据集特点自己调整。-- 这个有效果

• 在双线性部分引入Layer Norm效果可能会更好些

• 尝试在DNN部分使用残差防止DNN效果过差

• 直接取出Bilinear的输出结果然后上XGBoost，也就是说不用它来训练而是作为一种特征embedding操作去使用， 这个方法可能发生leak

• 在WDL上的调优经验： 适当调整DNN hideen layer之间的unit数量的减小比例，防止梯度爆炸/消失。

后记：

fibinet在我自己的任务上也试了下，确实会效果， 采用默认参数的话， 能和xdeepfm跑到同样的水平，而如果再稍微调调参， 就比xdeepfm要好些了。

参考：

• 论文原文
• FiBiNET: paper reading + 实践调优经验
• FiBiNET：结合特征重要性和双线性特征交互进行CTR预估
• FiBiNET(新浪)
• FiBiNet 网络介绍与源码浅析
• SENET双塔模型及应用