Top 55 Linked List Data Structure Interview Questions

You can also find all 55 answers here 👉 Devinterview.io - Linked List Data Structure

1. What is a Linked List?

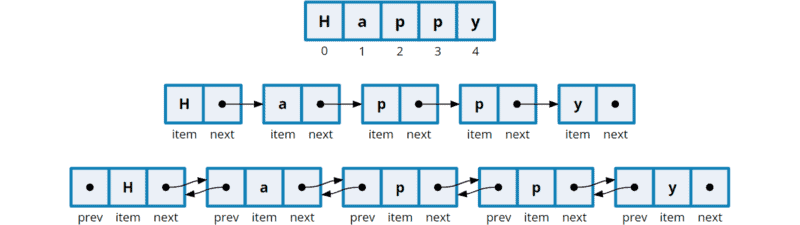
A Linked List is a dynamic data structure ideal for fast insertions and deletions. Unlike arrays, its elements aren't stored contiguously but are linked via pointers.

Anatomy of a Linked List

A Linked List is a collection of nodes, each having:

• Data: The stored value.
• Next Pointer: A reference to the next node.

The list starts with a Head node and ends with a node having a null Next pointer.

Visual Representation

Key Features

• Dynamic Size: Adapts to data volume.
• Non-Contiguous Memory: Flexibility in storage.
• Fast Insertions/Deletions: Limited pointer adjustments needed.

Types of Linked Lists

1. Singly Linked List: Each node has a single pointer to the next node. Traversal is unidirectional: from head to tail.
2. Doubly Linked List: Each node have two pointers: one pointing to the next node and another to the previous node. This allows for bidirectional traversal.
3. Circular Linked List: Like a singly linked list, but the tail node points back to the head, forming a loop.
4. Multi-level Linked List: This specialized type has nodes with multiple pointers, each pointing to different nodes. It's often used in advanced data structures like multi-level caches.

Common Operations and Time Complexity

• Traversal: Scan through nodes — $O(n)$.
• Insertion at the Beginning: Add a node at the start — $O(1)$.
• Insertion (other cases)/Deletion: Add or remove nodes elsewhere in the list — $O(n)$.
• Search: Locate specific nodes — $O(n)$.
• Sorting: Order or organize nodes in the list. Commonly-used algorithms for linked lists like merge sort have a time complexity of $O(n \log n)$.
• Merging: Combine two lists — $O(n)$ where $n$ is the total number of nodes in both lists.
• Reversal: Flip node order — $O(n)$.

Code Example: Singly Linked List

Here is the Python code:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class LinkedList:
    def __init__(self):
        self.head = None

    def insert(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
        else:
            last_node = self.head
            while last_node.next:
                last_node = last_node.next
            last_node.next = new_node

    def display(self):
        current = self.head
        while current:
            print(current.data)
            current = current.next

# Usage
my_list = LinkedList()
my_list.insert(1)
my_list.insert(2)
my_list.insert(3)
my_list.display()

# Output:
# 1
# 2
# 3

2. What are some pros and cons of Linked List compared to Arrays?

Let's look at the pros and cons of using linked lists compared to arrays.

Advantages of Linked Lists

• Dynamic Size: Linked lists naturally adjust to changing sizes, while arrays are fixed-sized. Dynamic arrays auto-resize but can lag in efficiency during frequent mid-list insertions or deletions.

• Efficient Insertions/Deletions: Insertions and deletions in linked lists only require a few pointer adjustments, whereas arrays may need shifting of elements.

• Flexibility in Size: Memory for nodes in linked lists is allocated or released as needed, potentially reducing memory wastage.

• Merging and Splitting: It's simpler to merge or split linked lists.

Disadvantages of Linked Lists

• Memory Overhead: Each node has overhead due to data and a pointer, using more memory than arrays for the same number of elements.

• Sequential Access: Linked lists only allow sequential access, unlike arrays that support direct indexing.

• Cache Inefficiency: Nodes might be scattered in memory, leading to cache misses.

• No Random Access: Element retrieval might require full list traversal, whereas arrays offer constant-time access.

• Data Integrity: If a node's link breaks, subsequent nodes are lost.

• Search Efficiency: Requires linear scans, which can be slower than searches in sorted arrays or trees.

• Sorting: Certain sorting algorithms, like QuickSort, are less efficient with linked lists than with arrays.

3. Explain the difference between Singly Linked Lists and Doubly Linked Lists.

Linked List variants, including Singly Linked Lists (SLL) and Doubly Linked Lists (DLL), each have unique characteristics when it comes to memory efficiency and traversal capabilities.

Key Distinctions

Memory Optimization

• Singly Linked List: Uses less memory per node as it requires only one reference to the next node.
• Doubly Linked List: Consumes more memory per node due to its need for two references, one each for the previous and next nodes.

Traversal Efficiency

• Singly Linked List: Traverseable in one direction, which is from the head to the tail.
• Doubly Linked List: Offers bi-directional traversability. You can move in both directions, from head to tail and vice versa.

Node Complexity

• Singly Linked List: Each node stores data and a reference to the next node.
• Doubly Linked List: In addition to data and pointers, each node maintains a reference to its previous node.

Visual Representation

Singly Linked List: Nodes link unidirectionally. Doubly Linked List: Nodes connect both ways, with arrows pointing in two directions.

Code Example: Singly Linked List

Here is the Python code:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class SinglyLinkedList:
    def __init__(self):
        self.head = None

    def add_node(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
        else:
            current = self.head
            while current.next:
                current = current.next
            current.next = new_node

# Instantiate and populate the Singly Linked List
sll = SinglyLinkedList()
sll.add_node(1)
sll.add_node(2)
sll.add_node(3)

Code Example: Doubly Linked List

Here is the Python code:

class Node:
    def __init__(self, data):
        self.data = data
        self.prev = None
        self.next = None

class DoublyLinkedList:
    def __init__(self):
        self.head = None

    def add_node(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
        else:
            current = self.head
            while current.next:
                current = current.next
            current.next = new_node
            new_node.prev = current

# Instantiate and populate the Doubly Linked List
dll = DoublyLinkedList()
dll.add_node(1)
dll.add_node(2)
dll.add_node(3)

4. How does a Linked List manage memory allocation differently from an Array?

Let's explore how linked lists and arrays differ in terms of memory management and their implications on data handling and computational complexity.

Memory Management

• Arrays: Contiguously allocate memory for predefined sizes. This results in efficient element access but may lead to memory wastage or reallocation drawbacks if storage requirements change.

• Linked Lists: Use dynamic memory allocation, where each node, containing data and a pointer, is allocated as needed. This flexibility in memory management is a key distinction from arrays.

Visual Representation

• Array: Elements are stored in contiguous memory cells or "slots," enabling direct $O(1)$ access based on the element index.

• Linked List: Nodes are disparate in memory, and connections between them unfold through pointers. Each node reserves memory addresses for the data it holds and for the subsequent node's memory address.

Array vs. Linked List Performance

Element Access

• Array: Elements are indexed, allowing direct access in $O(1)$ time, e.g., arr[5].
• Linked List: Sequential traversal is typically necessary, making element access linear in time or $O(n)$.

Memory Overhead

• Array: Offers direct memory access and is efficient for homogeneous data types.
• Linked List: Introduces memory overhead due to node pointer storage, but it's more adaptable for dynamic operations.

Insertion and Deletion

• Array: Can be $O(n)$ in the worst case due to potential shift or resize requirements.
• Linked List: Unquestionably efficient, typically $O(1)$, especially for list head or tail insertions.

Memory Allocation Efficacy

• Array: Might face underutilization or require resizing, introducing computational and memory overheads.
• Linked List: More efficient, with memory being dispatched as and when nodes are created or deleted.

Cache Efficiency and Data Locality

• Array: Due to contiguous memory, excels in cache and CPU caching optimization.
• Linked List: Might incur cache misses due to non-contiguous node storage, potentially leading to less efficient data retrieval in comparison to arrays.

5. What are the basic operations that can be performed on a Linked List?

Linked Lists are dynamic data structures optimized for insertion and deletion. Their key operations include:

Traversal

• Depiction: Visualize each node consecutively. Common implementations are iterative and recursive.
• Time Complexity: $O(n)$
• Code Example:

  def traverse(self):
      current = self.head
      while current:
          print(current.data)
          current = current.next

2. Search:

• Description: Identify a target value within the list. Requires traversal.
• Time Complexity: Best: $O(1)$; Worst: $O(n)$
• Code Example:

  def search(self, target):
      current = self.head
      while current:
          if current.data == target:
              return True
          current = current.next
      return False

3. Insertion:

• Description: Add a new node at a specified position.
• Time Complexity: Best: $O(1)$; Worst: $O(n)$, if tail needs to be found
• Code Example:

  def insert_at_start(self, data):
      new_node = Node(data)
      new_node.next = self.head
      self.head = new_node

4. Deletion:

• Description: Remove a node that contains a particular value, or from a specific position.
• Time Complexity: Best: $O(1)$ (for head or single known middle node); Worst: $O(n)$ (for removing tail before finding the new tail)
• Code Example:

  def delete_at_start(self):
      if self.head:
          self.head = self.head.next

5. Observations:
   • Iterative traversal is faster than recursive due to stack overhead.
   • Arraylist provides better search performance.
   • Linked lists are a top pick for frequent insertions or deletions at random positions.

6. What are some real-life Use Cases of Linked Lists?

Linked lists are widely used in real-world applications for their advantages in dynamic memory management and data manipulation.

Practical Applications

Operating Systems

• Task Scheduling: Linked lists efficiently manage queues of tasks awaiting execution.
• Memory Management: They facilitate dynamic memory allocation, especially useful in applications like memory pool management.

Text Editors

• Undo/Redo Functionality: Editors maintain a stack of changes using linked lists, enabling the undo and redo functionalities.

Music Players

• Playlists: Linked lists offer flexibility in managing playlists, allowing for the easy addition, deletion, and navigation of tracks.

Web Browsers

• Browser History: Linked lists, especially doubly linked ones, are instrumental in navigating web page histories, permitting both forward and backward traversal.

Compilers

• Symbol Tables: Compilers employ linked lists to manage tables containing variable and function identifiers. This provides scoped access to these identifiers during different stages of compilation.

Database Management Systems

• Transient Storage Structures: While core storage might use trees or hash indexes, linked lists can serve auxiliary roles, especially in in-memory databases.

Artificial Intelligence and Machine Learning

• Graph Representation: Algorithms requiring graph representations often utilize adjacency lists, essentially arrays of linked lists, to depict vertices and edges.

Caching Algorithms

• LRU Cache: Linked lists, particularly doubly linked ones, play a pivotal role in the Least Recently Used (LRU) caching algorithms to determine which items to replace.

Networking

• Packet Management: In networking scenarios, linked lists help manage queues of data packets awaiting transmission.

Gaming

• Character Inventory: In role-playing games, a character's inventory, where items are added and removed frequently, can be managed using linked lists.

7. When is a Circular Linked List useful?

A circular Linked List is a specific type of linked list where the tail node is intentionally connected back to the head node to form a closed loop.

Common Use Cases

• Emulating Circular Structures: Useful for representing naturally circular data like polygon vertices, buffer pools, or round-robin scheduling in operating systems.

• Queue Efficiency: Accessing the front and rear elements in constant time, improving queue implementations.

• Algorithmic Simplifications: Enables easier data manipulations like list splitting and concatenation in constant time.

Code Example: Queue Efficiency

Here is the Python code:

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

class CircularQueue:
    def __init__(self):
        self.front = self.rear = None

    def enqueue(self, data):
        new_node = Node(data)
        if self.rear:
            self.rear.next, self.rear = new_node, new_node
        else:
            self.front = self.rear = new_node
        self.rear.next = self.front

    def dequeue(self):
        if not self.front: return None
        if self.front == self.rear: self.front = self.rear = None
        else: self.front = self.front.next; self.rear.next = self.front
        return self.front.data if self.front else None

# Example usage:
cq = CircularQueue()
cq.enqueue(1); cq.enqueue(2); cq.enqueue(3)
print(cq.dequeue(), cq.dequeue(), cq.dequeue(), cq.dequeue())

8. When is Doubly Linked List more efficient than Singly Linked List?

Doubly linked lists offer advantages in specific use-cases but use more memory and may require more complex thread-safety

Key Efficiency Differences

• Deletion: If only the node to be deleted is known, doubly linked lists can delete it in $O(1)$ time, whereas singly linked lists may take up to $O(n)$ to find the prior node.

• Tail Operations: In doubly linked lists, tail-related tasks are $O(1)$. For singly linked lists without a tail pointer, these are $O(n)$.

Practical Use-Cases

• Cache Implementations: Doubly linked lists are ideal due to quick bidirectional insertion and deletion.

• Text Editors and Undo/Redo: The bidirectional capabilities make doubly linked lists more efficient for these functions.

9. Describe a scenario where the use of a Linked List is more suitable than a Dynamic Array.

Linked Lists and Dynamic Arrays are distinct data structures, each with its own advantages. Linked Lists, for instance, often outperform Dynamic Arrays in situations that involve frequent insertions and deletions.

Performance Considerations

• Insertion/Deletion: Linked Lists have $O(1)$ time complexity, whereas Dynamic Arrays are generally slower with an average $O(n)$ time complexity due to potential element shifts.
• Random Access: While Dynamic Arrays excel in $O(1)$ random access, Linked Lists have an inferior $O(n)$ complexity because they're not index-based.

Practical Scenario

Consider an interactive crossword puzzle game. For convenience, let's assume each crossword puzzle consists of 10 words. In the scenario, players:

1. Fill: Begin with a set of words at known positions.
2. Swap: Request to relocate words (Words 3 and 5, for example).
3. Expand/Contract: Add or remove a word, potentially changing its position in the list.

The Best Approach: To support these dynamic operations and maintain list integrity, a doubly-linked list is the most suitable choice.

10. Compare Array-based vs Linked List stack implementations.

Array-based stacks excel in time efficiency and direct element access. In contrast, linked list stacks are preferable for dynamic sizing and easy insertions or deletions.

Common Features

• Speed of Operations: Both pop and push are $O(1)$ operations.
• Memory Use: Both have $O(n)$ space complexity.
• Flexibility: Both can adapt their sizes, but their resizing strategies differ.

Key Distinctions

Array-Based Stack

• Locality: Consecutive memory locations benefit CPU caching.
• Random Access: Provides direct element access.
• Iterator Needs: Preferable if indexing or iterators are required.
• Performance: Slightly faster for top-element operations and potentially better for time-sensitive tasks due to caching.
• Push: $O(1)$ on average; resizing might cause occasional $O(n)$.

Linked List Stack

• Memory Efficiency: Better suited for fluctuating sizes and limited memory scenarios.
• Resizing Overhead: No resizing overheads.
• Pointer Overhead: Requires extra memory for storing pointers.

Code Example: Array-Based Stack

Here is the Python code:

class ArrayBasedStack:
    def __init__(self):
        self.stack = []
    def push(self, item):
        self.stack.append(item)
    def pop(self):
        return self.stack.pop() if self.stack else None

Code Example: Linked List Stack

Here is the Python code:

class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None
class LinkedListStack:
    def __init__(self):
        self.head = None
    def push(self, item):
        new_node = Node(item)
        new_node.next = self.head
        self.head = new_node
    def pop(self):
        if self.head:
            temp = self.head
            self.head = self.head.next
            return temp.data
        return None

11. How do Linked Lists perform in comparison with Trees for various operations?

Let's examine the time and space complexity of common operations in linked lists and trees, highlighting trade-offs of each data structure.

Common Data Structure Operations

Search

• Linked List: $O(n)$
• Tree: $O(\log n) \text{ to } O(n)$ - in case of linked list-like skewed trees.
  • Balanced Trees (e.g., AVL, Red-Black): $O(\log n)$
  • Unbalanced Trees: $O(n)$

Insert/Delete

• Linked List: $O(1)$ to $O(n)$ if searching is required before the operation.
• Tree: $O(\log n)$ to $O(n)$ in the worst-case (e.g., for skewed trees).

Operations at the Beginning/End

• Linked List: $O(1)$
  • Singly Linked List: $O(1)$
  • Doubly Linked List: $O(1)$
• Tree: Not applicable.

Operations in the Middle (based on the key or value)

• Linked List: $O(n)$

  To consider:

  • For the singly linked list, searching and finding the node before the target is involved leading to $O(n)$.
  • For the doubly linked list, direct access to the previous node reduces time to $O(1)$.

• Tree: $O(\log n)$ to $O(n)$

  The operation involves a search ($O(\log n)$ in a balanced tree) and then, if found, a constant-time to $O(\log n)$ modification (in case of tree balancing requirements).

Traversal

• Linked List: $O(n)$
• Tree: $O(n)$

Both data structures require visiting every element once.

12. When would you use a Linked List over a Hash Table?

Performance considerations and the nature of operations you plan to perform significantly influence whether a Linked List or a Hash Table best suits your needs.

Key Decision Factors

• Data Order and Relationship: Linked Lists fundamentally maintain order, which is often crucial in many scenarios. In contrast, Hash Tables impose no specific order.

• Memory Overhead: Linked Lists offer a more streamlined approach to memory management without the potential for clustering. Hash Tables, on the other hand, can have memory overhead due to hash functions, collision handling, and the need for extra space to prevent performance degradation.

• Access Time: Both data structures require $O(1)$ time complexity for certain operations. Hash Tables are known for this in most cases, but Linked Lists can be equally efficient for operations that take place solely at either end of the list.

• Duplication Handling: Linked Lists can directly store duplicate values. In Hash Tables, they can be tricky to manage because they require unique keys.

• Data Persistence and Disk Storage: Linked Lists are more conducive to persistent data storage, such as disk storage, because of their sequential data storage and easy disk access via pointers.

Use Case Considerations

Common Use Cases for Linked Lists

• Dynamic Allocation: When you need a dynamic allocation of memory that's not limited by fixed table sizes, Linked Lists can expand and contract efficiently.
• Efficient Insertions/Deletions: For these operations in the middle of a list, implementing them on Linked Lists is particularly straightforward and efficient.
• Sequential Data Processing: Certain tasks like linear search or the traversal of ordered data are simpler to perform with Linked Lists.
• Persistent Data Storage: When data persistence is a concern, such as for persistent caches, Log-structured File Systems, or databases with transaction logs.
• Memory Compactness: In scenarios where memory segmentation or disk access indirectly impacts performance, the undivided blocks in Linked Lists can be an advantageous choice.

Common Use Cases for Hash Tables

• Quick Lookups: For rapid retrieval of data based on a unique key, Hash Tables shine.
• Memory Mapped File Access: Especially beneficial for very large data sets when practical, as it can reduce I/O cost.
• Cache Performance: Their fast access and mutation operations make them ideal for in-memory caching systems.
• Distinct Value Storage: Best suited when each key must be unique. If you try to insert a duplicate key, its existing value is updated, which can be useful in multiple contexts, like address tables in a network.

13. Is it possible to Traverse a Linked List in O(n1/2)? (Jump Pointers).

While it may not be possible to traverse a linked list in better than $O(n)$ time complexity in the strictest sense, there are techniques that can make the traversal process more efficient in certain contexts.

In particular, let's explore the idea of "Jump Pointers" or "Square Root Jumps" which allows you to traverse a linked list in $O(\sqrt{n})$ time complexity.

What Are Jump Pointers?

Jump Pointers allow for quicker traversal by "jumping" over a fixed number of nodes $k$ during each step. This reduces the total number of nodes visited, thereby improving the time complexity.

For instance, when $k = \sqrt{n}$, the traversal time complexity drops to $O(\sqrt{n})$.

Code Example: Jump Pointers

Here is the Python code:

# Node definition
class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None

# LinkedList definition
class LinkedList:
    def __init__(self):
        self.head = None

    # Add node to end
    def append(self, data):
        new_node = Node(data)
        if not self.head:
            self.head = new_node
            return
        last = self.head
        while last.next:
            last = last.next
        last.next = new_node

    # Traverse using Jump Pointers
    def jump_traverse(self, jump_size):
        current = self.head
        while current:
            print(current.data)
            for _ in range(jump_size):
                if not current:
                    return
                current = current.next

# Create linked list and populate it
llist = LinkedList()
for i in range(1, 11):
    llist.append(i)

# Traverse using Jump Pointers
print("Jump Pointer Traversal:")
llist.jump_traverse(int(10**0.5))

14. How to apply Binary Search in O(log n) on a Sorted Linked List? (Skip Lists).

While Binary Search boasts a time complexity of $O(\log n)$, applying it to a singly linked list is less straightforward due to the list's linear nature and $O(n)$ access time. However, Skip Lists offer a clever workaround to achieve sub-linear search times in linked lists.

Why Traditional Binary Search Falls Short in Linked Lists

In a singly linked list, random access to elements is not possible. To reach the $k$-th element, you have to traverse $k-1$ preceding nodes. Therefore, the act of accessing a middle element during binary search incurs a time complexity of $O(n)$.

Skip Lists: A Solution for Sub-linear Search

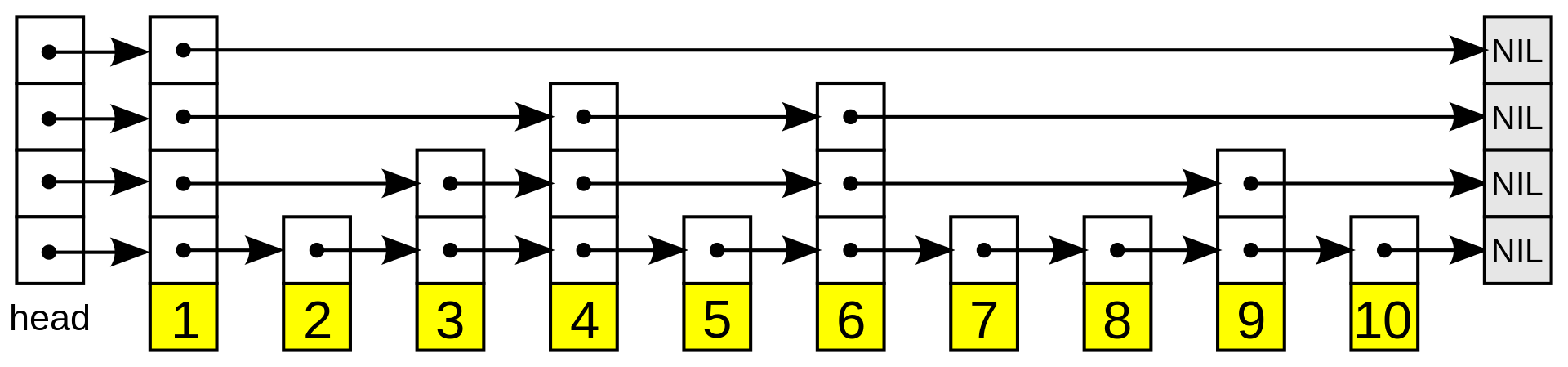
Skip Lists augment sorted linked lists with multiple layers of 'express lanes', allowing you to leapfrog over sections of the list. Each layer contains a subset of the elements from the layer below it, enabling faster search.

By starting at the topmost layer and working downwards, you can reduce the search space at each step. This results in an average time complexity of $O(\log n)$ for search operations.

Code Example: Visualizing a Skip List

Here is the Python code:

# Define a node for the Skip List
class SkipNode:
    def __init__(self, value):
        self.value = value
        self.next = []

# Initialize a Skip List
class SkipList:
    def __init__(self):
        self.head = SkipNode(float('-inf'))  # Initialize with the smallest possible value
        self.levels = 1  # Start with a single level

15. Is it possible to do Binary Search on a Doubly Linked List in O(n) time?

Applying Binary search to doubly-linked lists presents challenges because these lists lack the random access feature essential for binary search's efficiency.

In binary search, each comparison cuts the search space in half. However, accessing the middle element of a doubly-linked list takes $O(n)$ time since you have to traverse from the head or tail to the middle.

Consequently, the running time becomes $O(n \log n)$, not the optimal $O(\log n)$ seen with arrays.

Advanced Search Techniques for Doubly-Linked Lists

• Jump Pointers: Utilizes multiple pointers to skip predetermined numbers of nodes, enhancing traversal speed. Although it approximates a time complexity of $O(n)$, with a jump interval of $k$, the complexity improves to $O(n/k)$. However, this might increase memory usage.

• Interpolation Search: A modified binary search that employs linear interpolation for superior jumping efficiency in certain data distributions. Its worst-case time complexity is $O(n)$, but for uniformly distributed data, it can be as efficient as $O(\log \log n)$.

Code Example: Jump Pointers

Here is the Python code:

def jump_pointers_search(head, target):
    jump_factor = 2  
    current = head
    jump = head
    while current and current.value < target:
        jump = current
        for _ in range(jump_factor):
            if current.next:
                current = current.next
            else:
                break
    while jump and jump.value < target:
        jump = jump.next
    return jump

Code Example: Interpolation Search

Here is a Python code:

def interpolation_search(head, target):
    low = head
    high = None
    while low and low.value <= target:
        high = low
        low = low.next
    while high and high.value < target:
        high = high.next
    return high

Explore all 55 answers here 👉 Devinterview.io - Linked List Data Structure