by Changwoo Lee and Hun-Seok Kim from University of Michigan
An Official Implementation of Gaudi-GBLR, (G)eneralized (B)lock (L)ow-(R)ank Matrix with (Gau)ssian-(Di)richlet Function for End-to-End ViT and GPT Compression.
- 2024/01/16 Paper accepted to ICLR 2024!
Deep Neural Networks (DNNs) are getting bigger and bigger. A way to reduce the complexity of the DNNs is to use the structured weight matrices, like Low-Rank or Sparse matrices.
This repo introduces a Gaudi-GBLR matrix, which is a (G)eneralized (B)lock (L)ow-(R)ank Matrix with (Gau)ssian-(Di)richlet Function.
- Expressiveness. Gaudi-GBLR includes other structured matrices such as Low-Rank, Block-Low-Rank, and Block-Sparse matrices.
- Differentiability. The structure of the Gaudi-GBLR is differentiable! The efficient structure of the weight matrix is learned from data. So the efficient DNN can be learned from scratch!
- Layer-wise Optimization. The structure (and the complexity) is optimized in a layer-wise manner. The less important, the less complexity.
To this end, the efficient weight structures of the ViTs and GPT2 are found in this repo.
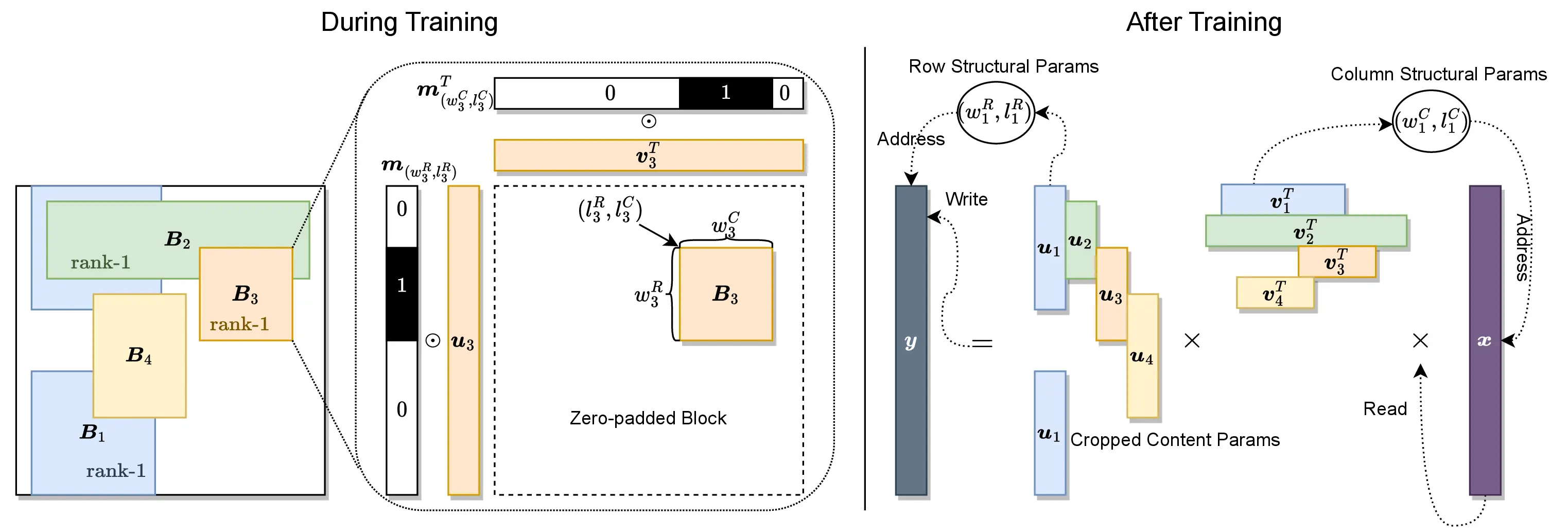
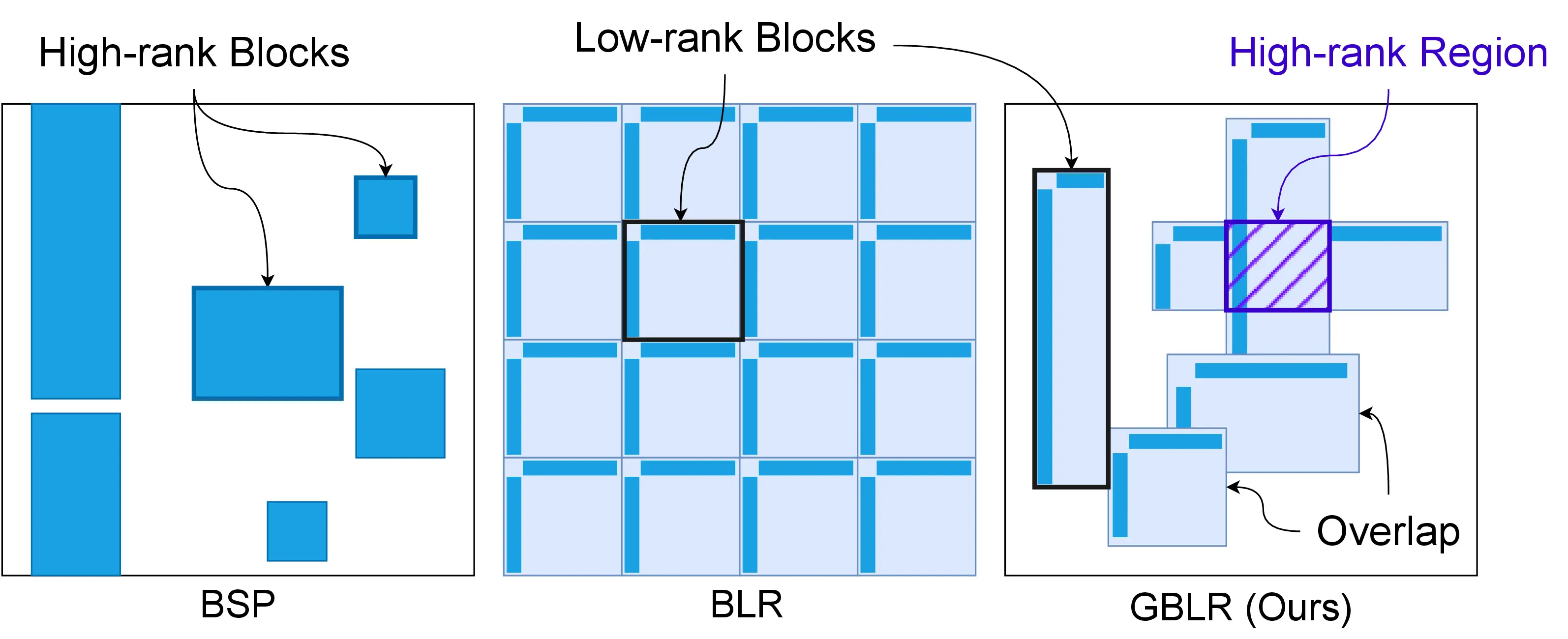
A GBLR matrix is a generalized version of the Block Low-Rank (BLR) matrix. Unlike the BLR structure, a GBLR matrix is composed of multiple overlapping low-rank blocks. Notably, the GBLR structure includes multiple important efficient matrix structures. In our paper, we analyzed that the GBLR format contains Low-Rank, Block-Sparse, Block-Low-Rank matrices of the same complexity for the matrix-vector product.
The key idea is to learn the location and the area of each block from data. Once they are found, the matrix-vector product can be done faster on the specialized hardware. We left demonstrating the actual speedup as future work.
Unfortunately, optimizing the structural (location and area) parameters of the GBLR matrix is not easy. The parameters are defined in the discrete space, and non-differentiable.
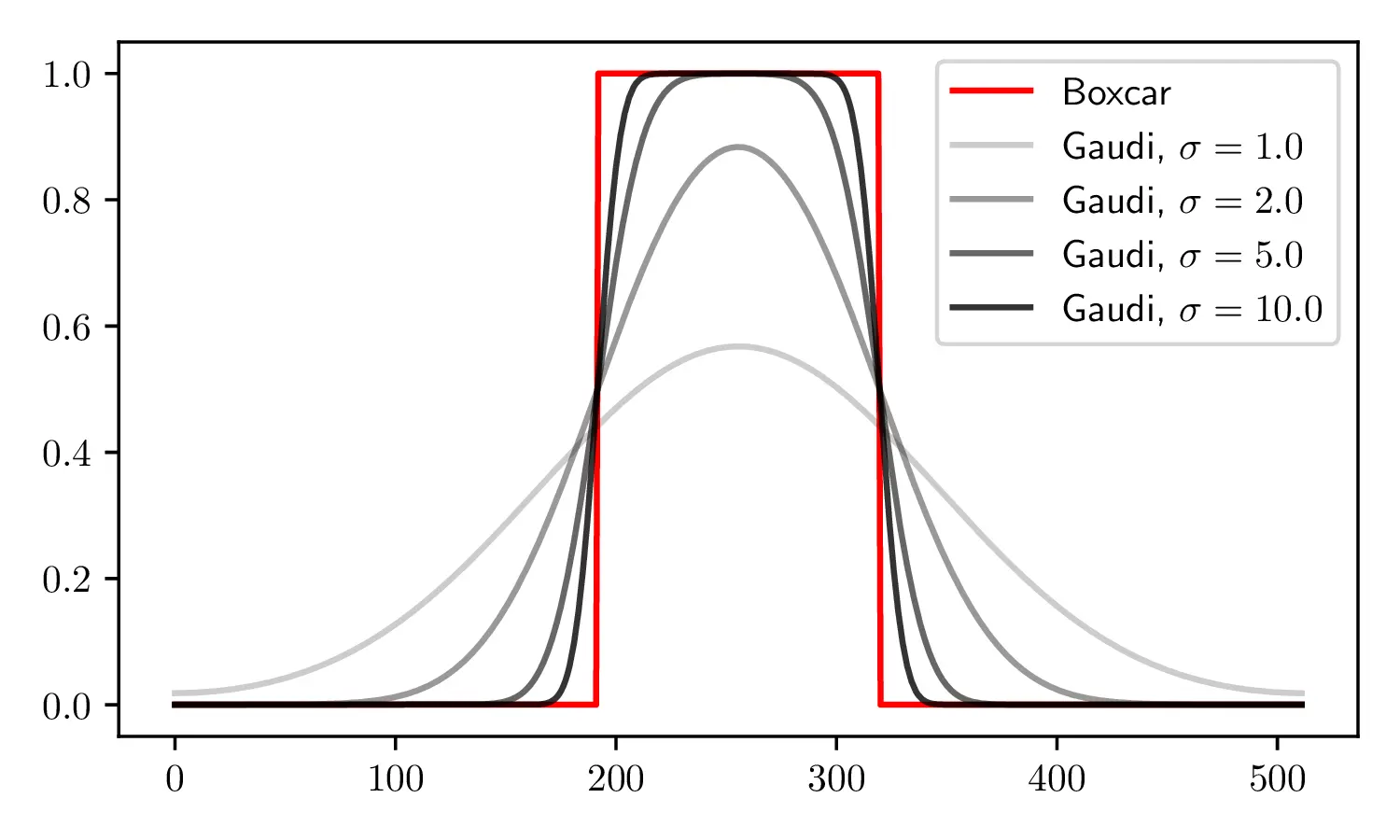
Here, we circumvent the problem by defining the structural parameter in the frequency domain. The location and the width and height of the low-rank block appear explicitly and differentiably in the form of the Dirichlet function, which is the DFT pair of the Boxcar function. By taking a Gaussian filter for the numerical stability, we obtain a Gaussian-Dirichlet (Gaudi) function to indicate the position of the low-rank block.
Intuitively, we don't think all layers are equally important. Some layers might contribute less than others, which indicates that less important layers can be compressed more.
Unfortunately, it has been very time-consuming to allocate different number of computations for each layer since the search space is discrete and the problem is NP-hard.
In contrast, with the GBLR format, the layer-wise structural parameter optimization can be easily done because we can update the structural parameters by Stochastic Gradient Descent (SGD).
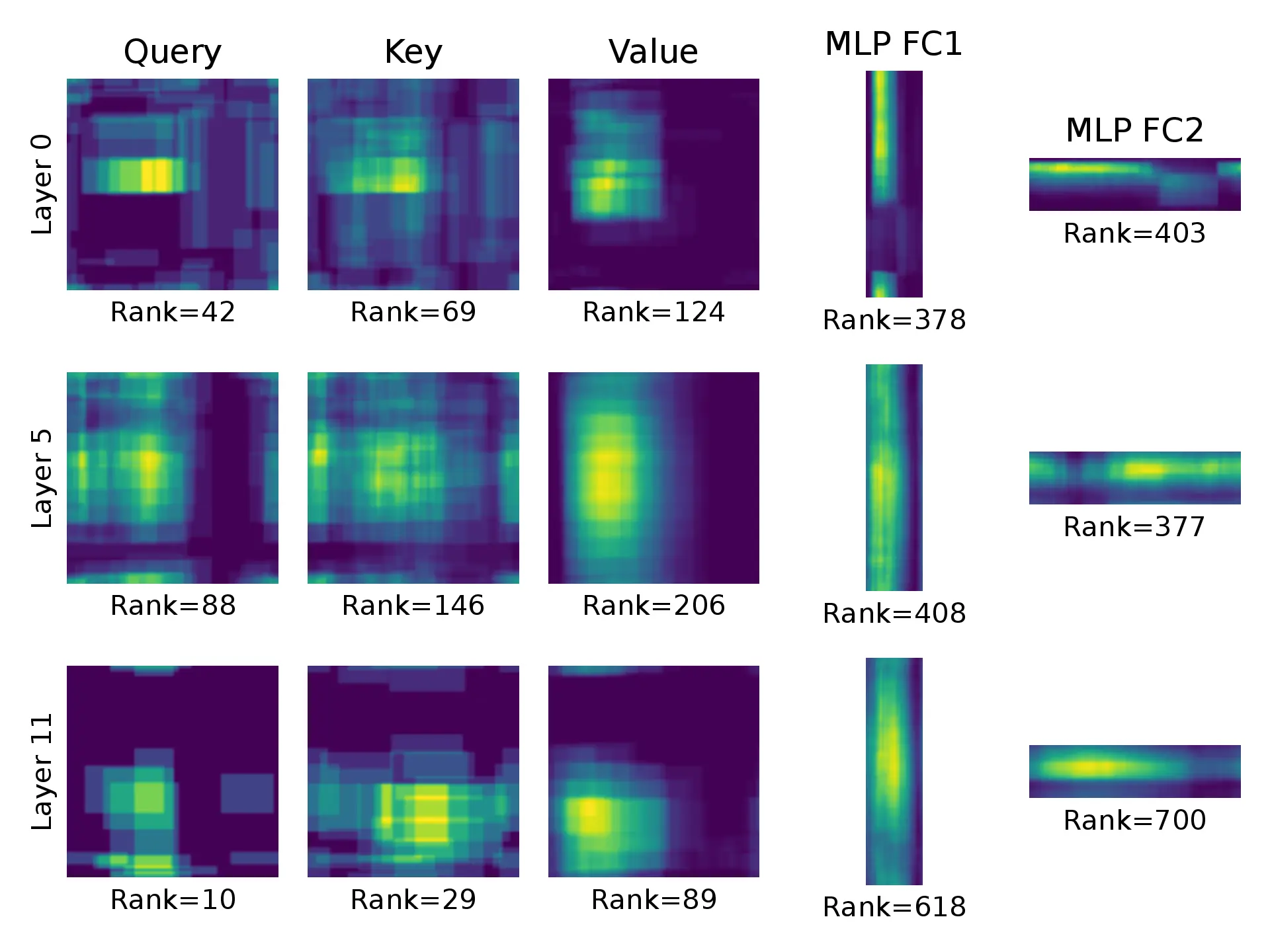
The figure below illustrates the learned Gaudi-GBLR weight matrices of the ViT-Base model trained on ImageNet. The brighter, the more overlapping low-rank blocks. Each weight has different rank and structure, which are found during the training process by SGD.
Please refer to environment.yml for the full dependency list.
An environment variable PROJECT_ROOT='./' must be set beforehand.
The ImageNet dataset is assumed to be prepared in ./data/imagenet.
Otherwise, User can specify the path by datamodule.data_path=PATH_TO_DATASET.
The project downloads the WikiText103 and CIFAR-10/100 datasets automatically.
| Model | Accuracy | FLOPs | Link |
|---|---|---|---|
| ViT-B-Gaudi-GBLR | 78.51% | 5.65G | link |
| ResNet18-Gaudi-GBLR | 69.31% | 1.01G | link |
| Model | Perplexity | Relative FLOPs | Link |
|---|---|---|---|
| GPT2-Gaudi-GBLR | 18.99 | 43.7% | link |
All scripts can be found in ./scripts/.
Assuming that the ImageNet baseline ViT-Base model obtained in 1. is saved in ./saved_models/imagenet-vit-b/last.ckpt:
python3 run.py experiment=imagenet/vit/vit-b-gaudi-finetune callbacks.init_from_pretrained.budget=0.15 callbacks.init_from_pretrained.ckpt=./saved_models/imagenet-vit-b/last.ckptpython3 run.py experiment=wt103/gpt2-ft-gaudi trainer.devices=2 model.layer_type='gaudi' datamodule.batch_size=8 trainer.strategy="ddp" model.model_name="gpt2" model.gaudi_params.no_gaussian=Truepython3 run.py experiment=imagenet/vit/vit-b-gaudi callbacks.shrink.thres=0.04 callbacks.shrink.target_width=0.12 trainer.devices=8 +trainer.strategy="ddp" This repo is heavily based on the Monarch / Pixelated Butterfly project from Hazy Research (https://github.com/HazyResearch/fly). Check out their amazing research projects!
Please cite our work if it helps your project.
@article{lee2023differentiable,
title={Differentiable Learning of Generalized Structured Matrices for Efficient Deep Neural Networks},
author={Lee, Changwoo and Kim, Hun-Seok},
journal={arXiv preprint arXiv:2310.18882},
year={2023}
}