-
Notifications
You must be signed in to change notification settings - Fork 21
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
15 changed files
with
572 additions
and
0 deletions.
There are no files selected for viewing
15 changes: 15 additions & 0 deletions
15
src/main/kotlin/g3001_3100/s3065_minimum_operations_to_exceed_threshold_value_i/Solution.kt
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,15 @@ | ||
| package g3001_3100.s3065_minimum_operations_to_exceed_threshold_value_i | ||
|
|
||
| // #Easy #Array #2024_03_31_Time_180_ms_(71.76%)_Space_36.9_MB_(81.18%) | ||
|
|
||
| class Solution { | ||
| fun minOperations(nums: IntArray, k: Int): Int { | ||
| var count = 0 | ||
| for (num in nums) { | ||
| if (num >= k) { | ||
| count++ | ||
| } | ||
| } | ||
| return nums.size - count | ||
| } | ||
| } |
48 changes: 48 additions & 0 deletions
48
...otlin/g3001_3100/s3065_minimum_operations_to_exceed_threshold_value_i/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,48 @@ | ||
| 3065\. Minimum Operations to Exceed Threshold Value I | ||
|
|
||
| Easy | ||
|
|
||
| You are given a **0-indexed** integer array `nums`, and an integer `k`. | ||
|
|
||
| In one operation, you can remove one occurrence of the smallest element of `nums`. | ||
|
|
||
| Return _the **minimum** number of operations needed so that all elements of the array are greater than or equal to_ `k`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [2,11,10,1,3], k = 10 | ||
|
|
||
| **Output:** 3 | ||
|
|
||
| **Explanation:** After one operation, nums becomes equal to [2, 11, 10, 3]. | ||
|
|
||
| After two operations, nums becomes equal to [11, 10, 3]. | ||
|
|
||
| After three operations, nums becomes equal to [11, 10]. | ||
|
|
||
| At this stage, all the elements of nums are greater than or equal to 10 so we can stop. | ||
|
|
||
| It can be shown that 3 is the minimum number of operations needed so that all elements of the array are greater than or equal to 10. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [1,1,2,4,9], k = 1 | ||
|
|
||
| **Output:** 0 | ||
|
|
||
| **Explanation:** All elements of the array are greater than or equal to 1 so we do not need to apply any operations on nums. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| **Input:** nums = [1,1,2,4,9], k = 9 | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** only a single element of nums is greater than or equal to 9 so we need to apply the operations 4 times on nums. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `1 <= nums.length <= 50` | ||
| * <code>1 <= nums[i] <= 10<sup>9</sup></code> | ||
| * <code>1 <= k <= 10<sup>9</sup></code> | ||
| * The input is generated such that there is at least one index `i` such that `nums[i] >= k`. |
36 changes: 36 additions & 0 deletions
36
src/main/kotlin/g3001_3100/s3066_minimum_operations_to_exceed_threshold_value_ii/Solution.kt
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,36 @@ | ||
| package g3001_3100.s3066_minimum_operations_to_exceed_threshold_value_ii | ||
|
|
||
| // #Medium #Array #Heap_Priority_Queue #Simulation | ||
| // #2024_03_31_Time_543_ms_(98.11%)_Space_73.7_MB_(86.79%) | ||
|
|
||
| class Solution { | ||
| fun minOperations(nums: IntArray, k: Int): Int { | ||
| val n = nums.size | ||
| var steps = 0 | ||
| nums.sort() | ||
| val extra: MutableList<Int> = ArrayList() | ||
| var i = 0 | ||
| var j = 0 | ||
| while ((i < n && nums[i] < k) || (j < extra.size && extra[j] < k)) { | ||
| val min = if (i < n && (j >= extra.size || extra[j] > nums[i])) { | ||
| nums[i++] | ||
| } else { | ||
| extra[j++] | ||
| } | ||
| val max = if (i < n && (j >= extra.size || extra[j] > nums[i])) { | ||
| nums[i++] | ||
| } else { | ||
| extra[j++] | ||
| } | ||
| steps++ | ||
| var res = min.toLong() | ||
| res = 2 * res + max | ||
| if (res > Int.MAX_VALUE) { | ||
| extra.add(Int.MAX_VALUE) | ||
| } else { | ||
| extra.add(res.toInt()) | ||
| } | ||
| } | ||
| return steps | ||
| } | ||
| } |
54 changes: 54 additions & 0 deletions
54
...tlin/g3001_3100/s3066_minimum_operations_to_exceed_threshold_value_ii/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,54 @@ | ||
| 3066\. Minimum Operations to Exceed Threshold Value II | ||
|
|
||
| Medium | ||
|
|
||
| You are given a **0-indexed** integer array `nums`, and an integer `k`. | ||
|
|
||
| In one operation, you will: | ||
|
|
||
| * Take the two smallest integers `x` and `y` in `nums`. | ||
| * Remove `x` and `y` from `nums`. | ||
| * Add `min(x, y) * 2 + max(x, y)` anywhere in the array. | ||
|
|
||
| **Note** that you can only apply the described operation if `nums` contains at least two elements. | ||
|
|
||
| Return _the **minimum** number of operations needed so that all elements of the array are greater than or equal to_ `k`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [2,11,10,1,3], k = 10 | ||
|
|
||
| **Output:** 2 | ||
|
|
||
| **Explanation:** In the first operation, we remove elements 1 and 2, then add 1 \* 2 + 2 to nums. nums becomes equal to [4, 11, 10, 3]. | ||
|
|
||
| In the second operation, we remove elements 3 and 4, then add 3 \* 2 + 4 to nums. nums becomes equal to [10, 11, 10]. | ||
|
|
||
| At this stage, all the elements of nums are greater than or equal to 10 so we can stop. | ||
|
|
||
| It can be shown that 2 is the minimum number of operations needed so that all elements of the array are greater than or equal to 10. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [1,1,2,4,9], k = 20 | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** After one operation, nums becomes equal to [2, 4, 9, 3]. | ||
|
|
||
| After two operations, nums becomes equal to [7, 4, 9]. | ||
|
|
||
| After three operations, nums becomes equal to [15, 9]. | ||
|
|
||
| After four operations, nums becomes equal to [33]. | ||
|
|
||
| At this stage, all the elements of nums are greater than 20 so we can stop. | ||
|
|
||
| It can be shown that 4 is the minimum number of operations needed so that all elements of the array are greater than or equal to 20. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>2 <= nums.length <= 2 * 10<sup>5</sup></code> | ||
| * <code>1 <= nums[i] <= 10<sup>9</sup></code> | ||
| * <code>1 <= k <= 10<sup>9</sup></code> | ||
| * The input is generated such that an answer always exists. That is, there exists some sequence of operations after which all elements of the array are greater than or equal to `k`. |
58 changes: 58 additions & 0 deletions
58
...3001_3100/s3067_count_pairs_of_connectable_servers_in_a_weighted_tree_network/Solution.kt
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,58 @@ | ||
| package g3001_3100.s3067_count_pairs_of_connectable_servers_in_a_weighted_tree_network | ||
|
|
||
| // #Medium #Array #Depth_First_Search #Tree #2024_03_31_Time_578_ms_(83.33%)_Space_59.5_MB_(45.83%) | ||
|
|
||
| @Suppress("NAME_SHADOWING") | ||
| class Solution { | ||
| private lateinit var adj: Array<ArrayList<Int>> | ||
|
|
||
| fun countPairsOfConnectableServers(edges: Array<IntArray>, signalSpeed: Int): IntArray { | ||
| val n = edges.size + 1 | ||
| adj = Array(n) { ArrayList() } | ||
| for (i in 0 until n) { | ||
| adj[i] = ArrayList() | ||
| } | ||
| for (edge in edges) { | ||
| val u = edge[0] | ||
| val v = edge[1] | ||
| val w = edge[2] | ||
| adj[u].add(v) | ||
| adj[v].add(u) | ||
| adj[u].add(w) | ||
| adj[v].add(w) | ||
| } | ||
| val res = IntArray(n) | ||
| for (i in 0 until n) { | ||
| if (adj[i].size > 2) { | ||
| val al = ArrayList<Int>() | ||
| var j = 0 | ||
| while (j < adj[i].size) { | ||
| val cnt = IntArray(1) | ||
| dfs(adj[i][j], i, adj[i][j + 1], cnt, signalSpeed) | ||
| al.add(cnt[0]) | ||
| j += 2 | ||
| } | ||
| var sum = 0 | ||
| for (j in al) { | ||
| res[i] += (sum * j) | ||
| sum += j | ||
| } | ||
| } | ||
| } | ||
| return res | ||
| } | ||
|
|
||
| fun dfs(node: Int, par: Int, sum: Int, cnt: IntArray, ss: Int) { | ||
| if (sum % ss == 0) { | ||
| cnt[0]++ | ||
| } | ||
| var i = 0 | ||
| while (i < adj[node].size) { | ||
| val child = adj[node][i] | ||
| if (child != par) { | ||
| dfs(child, node, sum + adj[node][i + 1], cnt, ss) | ||
| } | ||
| i += 2 | ||
| } | ||
| } | ||
| } |
51 changes: 51 additions & 0 deletions
51
...0/s3067_count_pairs_of_connectable_servers_in_a_weighted_tree_network/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,51 @@ | ||
| 3067\. Count Pairs of Connectable Servers in a Weighted Tree Network | ||
|
|
||
| Medium | ||
|
|
||
| You are given an unrooted weighted tree with `n` vertices representing servers numbered from `0` to `n - 1`, an array `edges` where <code>edges[i] = [a<sub>i</sub>, b<sub>i</sub>, weight<sub>i</sub>]</code> represents a bidirectional edge between vertices <code>a<sub>i</sub></code> and <code>b<sub>i</sub></code> of weight <code>weight<sub>i</sub></code>. You are also given an integer `signalSpeed`. | ||
|
|
||
| Two servers `a` and `b` are **connectable** through a server `c` if: | ||
|
|
||
| * `a < b`, `a != c` and `b != c`. | ||
| * The distance from `c` to `a` is divisible by `signalSpeed`. | ||
| * The distance from `c` to `b` is divisible by `signalSpeed`. | ||
| * The path from `c` to `b` and the path from `c` to `a` do not share any edges. | ||
|
|
||
| Return _an integer array_ `count` _of length_ `n` _where_ `count[i]` _is the **number** of server pairs that are **connectable** through_ _the server_ `i`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
|  | ||
|
|
||
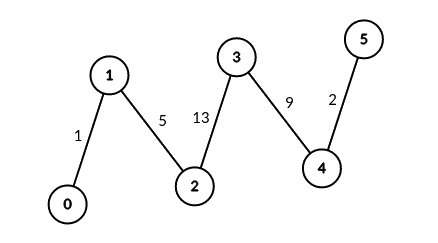
| **Input:** edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1 | ||
|
|
||
| **Output:** [0,4,6,6,4,0] | ||
|
|
||
| **Explanation:** Since signalSpeed is 1, count[c] is equal to the number of pairs of paths that start at c and do not share any edges. | ||
|
|
||
| In the case of the given path graph, count[c] is equal to the number of servers to the left of c multiplied by the servers to the right of c. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| 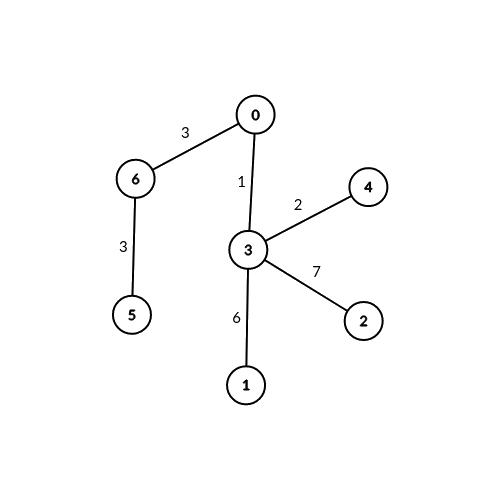 | ||
|
|
||
| **Input:** edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3 | ||
|
|
||
| **Output:** [2,0,0,0,0,0,2] | ||
|
|
||
| **Explanation:** Through server 0, there are 2 pairs of connectable servers: (4, 5) and (4, 6). | ||
|
|
||
| Through server 6, there are 2 pairs of connectable servers: (4, 5) and (0, 5). | ||
|
|
||
| It can be shown that no two servers are connectable through servers other than 0 and 6. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `2 <= n <= 1000` | ||
| * `edges.length == n - 1` | ||
| * `edges[i].length == 3` | ||
| * <code>0 <= a<sub>i</sub>, b<sub>i</sub> < n</code> | ||
| * <code>edges[i] = [a<sub>i</sub>, b<sub>i</sub>, weight<sub>i</sub>]</code> | ||
| * <code>1 <= weight<sub>i</sub> <= 10<sup>6</sup></code> | ||
| * <code>1 <= signalSpeed <= 10<sup>6</sup></code> | ||
| * The input is generated such that `edges` represents a valid tree. |
24 changes: 24 additions & 0 deletions
24
src/main/kotlin/g3001_3100/s3068_find_the_maximum_sum_of_node_values/Solution.kt
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,24 @@ | ||
| package g3001_3100.s3068_find_the_maximum_sum_of_node_values | ||
|
|
||
| // #Hard #Array #Dynamic_Programming #Sorting #Greedy #Tree #Bit_Manipulation | ||
| // #2024_03_31_Time_531_ms_(66.67%)_Space_64.9_MB_(66.67%) | ||
|
|
||
| import kotlin.math.abs | ||
| import kotlin.math.max | ||
| import kotlin.math.min | ||
|
|
||
| @Suppress("UNUSED_PARAMETER") | ||
| class Solution { | ||
| fun maximumValueSum(nums: IntArray, k: Int, edges: Array<IntArray?>?): Long { | ||
| var res: Long = 0 | ||
| var d = 1 shl 30 | ||
| var c = 0 | ||
| for (a in nums) { | ||
| val b = a xor k | ||
| res += max(a, b) | ||
| c = c xor if (a < b) 1 else 0 | ||
| d = min(d, abs((a - b))) | ||
| } | ||
| return res - d * c | ||
| } | ||
| } |
65 changes: 65 additions & 0 deletions
65
src/main/kotlin/g3001_3100/s3068_find_the_maximum_sum_of_node_values/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,65 @@ | ||
| 3068\. Find the Maximum Sum of Node Values | ||
|
|
||
| Hard | ||
|
|
||
| There exists an **undirected** tree with `n` nodes numbered `0` to `n - 1`. You are given a **0-indexed** 2D integer array `edges` of length `n - 1`, where <code>edges[i] = [u<sub>i</sub>, v<sub>i</sub>]</code> indicates that there is an edge between nodes <code>u<sub>i</sub></code> and <code>v<sub>i</sub></code> in the tree. You are also given a **positive** integer `k`, and a **0-indexed** array of **non-negative** integers `nums` of length `n`, where `nums[i]` represents the **value** of the node numbered `i`. | ||
|
|
||
| Alice wants the sum of values of tree nodes to be **maximum**, for which Alice can perform the following operation **any** number of times (**including zero**) on the tree: | ||
|
|
||
| * Choose any edge `[u, v]` connecting the nodes `u` and `v`, and update their values as follows: | ||
| * `nums[u] = nums[u] XOR k` | ||
| * `nums[v] = nums[v] XOR k` | ||
|
|
||
| Return _the **maximum** possible **sum** of the **values** Alice can achieve by performing the operation **any** number of times_. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| 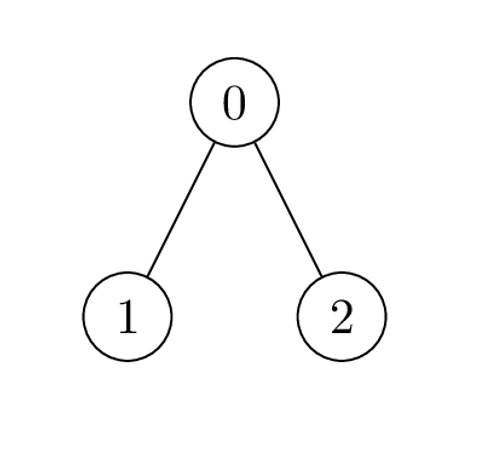 | ||
|
|
||
| **Input:** nums = [1,2,1], k = 3, edges = [[0,1],[0,2]] | ||
|
|
||
| **Output:** 6 | ||
|
|
||
| **Explanation:** Alice can achieve the maximum sum of 6 using a single operation: | ||
|
|
||
| - Choose the edge [0,2]. nums[0] and nums[2] become: 1 XOR 3 = 2, and the array nums becomes: [1,2,1] -> [2,2,2]. | ||
|
|
||
| The total sum of values is 2 + 2 + 2 = 6. | ||
|
|
||
| It can be shown that 6 is the maximum achievable sum of values. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| 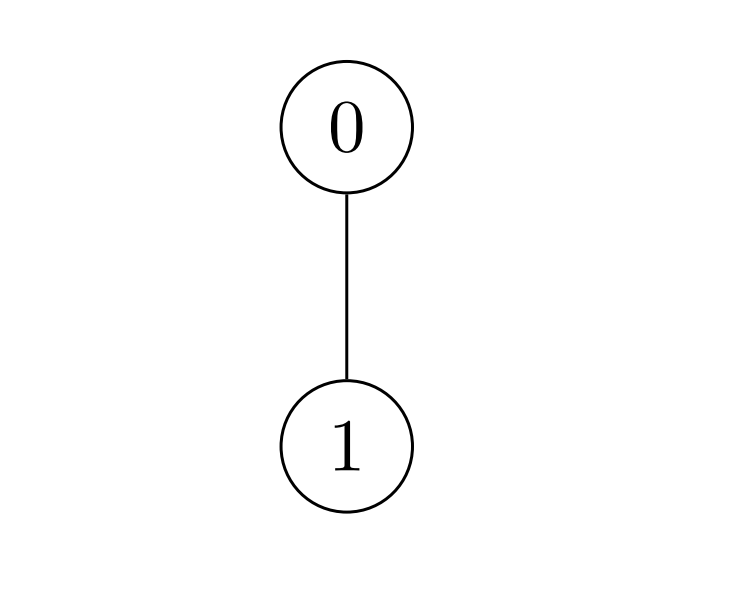 | ||
|
|
||
| **Input:** nums = [2,3], k = 7, edges = [[0,1]] | ||
|
|
||
| **Output:** 9 | ||
|
|
||
| **Explanation:** Alice can achieve the maximum sum of 9 using a single operation: | ||
|
|
||
| - Choose the edge [0,1]. nums[0] becomes: 2 XOR 7 = 5 and nums[1] become: 3 XOR 7 = 4, and the array nums becomes: [2,3] -> [5,4]. | ||
|
|
||
| The total sum of values is 5 + 4 = 9. | ||
|
|
||
| It can be shown that 9 is the maximum achievable sum of values. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| 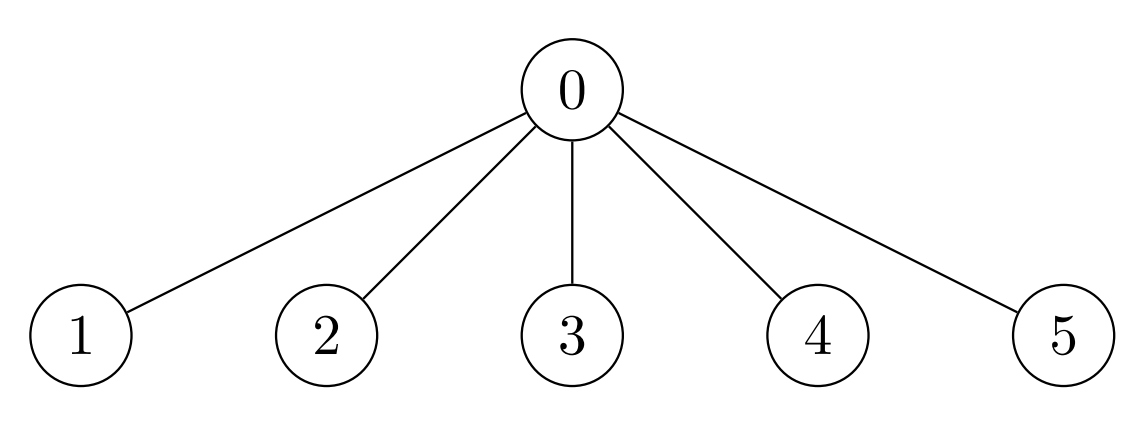 | ||
|
|
||
| **Input:** nums = [7,7,7,7,7,7], k = 3, edges = [[0,1],[0,2],[0,3],[0,4],[0,5]] | ||
|
|
||
| **Output:** 42 | ||
|
|
||
| **Explanation:** The maximum achievable sum is 42 which can be achieved by Alice performing no operations. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>2 <= n == nums.length <= 2 * 10<sup>4</sup></code> | ||
| * <code>1 <= k <= 10<sup>9</sup></code> | ||
| * <code>0 <= nums[i] <= 10<sup>9</sup></code> | ||
| * `edges.length == n - 1` | ||
| * `edges[i].length == 2` | ||
| * `0 <= edges[i][0], edges[i][1] <= n - 1` | ||
| * The input is generated such that `edges` represent a valid tree. |
32 changes: 32 additions & 0 deletions
32
src/main/kotlin/g3001_3100/s3069_distribute_elements_into_two_arrays_i/Solution.kt
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,32 @@ | ||
| package g3001_3100.s3069_distribute_elements_into_two_arrays_i | ||
|
|
||
| // #Easy #Array #Simulation #2024_03_31_Time_207_ms_(96.92%)_Space_37.5_MB_(87.69%) | ||
|
|
||
| class Solution { | ||
| fun resultArray(nums: IntArray): IntArray { | ||
| var s = 0 | ||
| var t = 1 | ||
| for (i in 2 until nums.size) { | ||
| var p = i | ||
| if (nums[s] > nums[t]) { | ||
| for (q in s + 1 until i) { | ||
| val temp = nums[p] | ||
| nums[p] = nums[p - 1] | ||
| nums[p - 1] = temp | ||
| p -= 1 | ||
| } | ||
| s++ | ||
| t++ | ||
| } else { | ||
| for (q in t + 1 until i) { | ||
| val temp = nums[p] | ||
| nums[p] = nums[p - 1] | ||
| nums[p - 1] = temp | ||
| p -= 1 | ||
| } | ||
| t++ | ||
| } | ||
| } | ||
| return nums | ||
| } | ||
| } |
Oops, something went wrong.