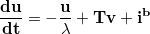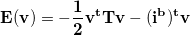This Hopfield Network Toolbox is mainly focused in Continuous Hopfield Networks (CHNs). This Toolbox is based on the work by Javier Yáñez, Pedro M. Talaván and Lucas García.
The Continuous Hopfield Network (CHN) is a recurrent neural network with an associated differential equation, whose state evolves from an initial condition to an equilibrium point by minimizing a Lyapunov function. As the Lyapunov function is associated with an objective function of the optimization problem (i.e. the mapping process), the equilibrium, or stable point, helps identify a local optimum for the optimization problem. The dynamics of the CHN is described by a differential equation:
and the output function is a hyperbolic tangent:
The existence of an equilibrium point is guaranteed if a Lyapunov or energy function exists. The idea is that the network's Lyapunov function, when 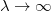
The CHN will solve those combinatorial problems which can be expressed as the constrained minimization of:
However, at this point the Hopfield Network Toolbox is primarily designed to solve the Traveling Salesman Proble,.
It is recommended to use the latest release. You may download the entire source code or a single installable Toolbox file.
If you have downloaded the source code, simply run
>> setup_hopfieldNetworkin MATLAB's Command Window to add all the right paths.
If you have downloaded the .mltbx file, double click it from within MATLAB to install the Toolbox.
Want to contribute? Great! Feel free to fork the repository and contact us for instructions and suggestions.
Open a new Issue and label it as a question. We will get back to you.
- “Neural” computation of decisions in optimization problems
- A continuous Hopfield network equilibrium points algorithm
- Parameter setting of the Hopfield network applied to TSP
- Improving the Hopfield model performance when applied to the traveling salesman problem: A divide-and-conquer scheme
- Attractor basin analysis of the Hopfield model: The Generalized Quadratic Knapsack Problem. In International Work-Conference on Artificial Neural Networks (2017)
Send us an Email with your comments/suggestions.
BSD 2-clause “Simplified” License