This is just (probaby outdated) HTML copy of the actual IPyhton Notebook. Please consider viewing the PyDENN.ipynb instead.
import numpy as np
import math
from itertools import permutations
from collections import namedtupleArtificial Neural Networks (ANNs for short) have become really useful tool lately. Although they were introduced aready in the 1950s, the progress in training methodologies and computational resources have recently make amazing new applications possible. In this notebook I will give a short introduction to neural networks and give an non-canonical example in training them.
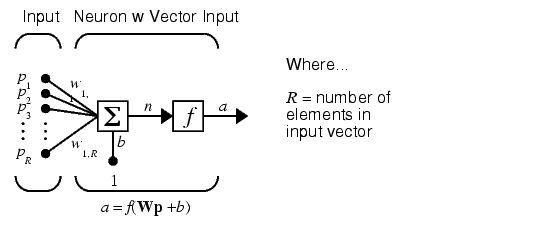
ANN cosists of neurons, which are usually interconnected with neurons in the previous neuron layer. Each connection carries a weight, and in addition there is a bias factor and weight. The weighted inputs of a neuron are summed with the bias and an activation function is used to scale its output. Lets implement one.
Layer = namedtuple('Layer', 'weights act_fun')
def calc_neuron_val(vals, weights, bias):
return np.dot(vals, weights)+1.0*bias
def eval_neural_net(all_layers, input_vec):
prev_layer_vec = input_vec
for layer in all_layers:
# Evaluate all neurons on this layer on one go with
# functional style map.
layer_vals = layer.act_fun(
list(map(lambda neuron_weights:
calc_neuron_val(prev_layer_vec,
neuron_weights[:-1],
neuron_weights[-1]),
layer.weights)) )
prev_layer_vec = layer_vals
return layer_vals Yes, it is as simple as that. The calc_neuron_val evaluates the output of a single neuron given a vector of input values (vals) with the weights and bias. Evaluating the entire neural network is equally simple. Then it is just the matter of propagating the output weights of the previous layer (or inputs on the first layer) as inputs of the next layer until the final output emerges.
*Image source: matlab.izmiran.ru*
# Example: create a neural network with 3 inputs and 1 output.
# It has 2 hidden layers (with sizes of 5 and 3 neurons)
ninputs = 3
noutputs = 1
example_nnet = [Layer(np.random.rand(5, ninputs+1)*2-1, np.tanh),
Layer(np.random.rand(3, 5+1)*2-1, np.tanh),
Layer(np.random.rand(noutputs, 3+1)*2-1, np.tanh)]
# Evaluate the neural network with some input
print( eval_neural_net(example_nnet, [1.1,2.2,3.3]) )[-0.65098949]
Read the classical machine learning iris dataset from a text file. The dataset contains the measured length and the width of sepals and petals of 150 flower samples. There exists three types of flowers in the dataset.
After reading the data, make a variable containing a set of classes, and a dictionary which maps a numerical (integer) vote to the corresponding category label (which may be text or something else).
dataset = np.genfromtxt('iris.data.txt', delimiter=',', dtype=None, encoding='ascii')
classes = set( e[-1] for e in dataset )
nclasses = len(classes)
ninputs = len(dataset[0])-1
class_to_vote = dict(zip(classes, range(nclasses)))
correct_answers = np.asarray([class_to_vote[e[-1]] for e in dataset])
print( "Data looks like this:" )
print( dataset[[0,75,125]] )
print()
print( "It has following %d classes %s and %d input values"%\
(nclasses, ", ".join(str(c) for c in classes), ninputs) )
print()
print( "The labels are mapped to vote indices like this:" )
print( class_to_vote )
# Split the dataset to training / testing data by 50%/50%
training_dataset = dataset[::2] #even
testing_dataset = dataset[1::2] #odd
training_answers = correct_answers[::2] #even
testing_answers = correct_answers[1::2] #oddData looks like this:
[(5.1, 3.5, 1.4, 0.2, 'Iris-setosa')
(6.6, 3. , 4.4, 1.4, 'Iris-versicolor')
(7.2, 3.2, 6. , 1.8, 'Iris-virginica')]
It has following 3 classes Iris-virginica, Iris-setosa, Iris-versicolor and 4 input values
The labels are mapped to vote indices like this:
{'Iris-virginica': 0, 'Iris-setosa': 1, 'Iris-versicolor': 2}
ANN maps real valued input to real valued output. To use ANN as a classifier, we must discretize the output. One way to do this is to have as many outputs as there are classes (in our case flower species) and let the highest value of these three outputs to decide the class.
The code below allows a simple multilayer artificial neural network to used as a classifier. The find_initial_nn_classifier function generates a randomly initialized ANN with the specified architecture (layer sizes) and activation functions.
def nn_votes(all_layers, dataset):
votes = []
for data in dataset:
data = data.tolist()
label, input_vec = (data[-1], data[:-1])
try:
output = eval_neural_net(all_layers, input_vec)
except:
print( label, input_vec )
break
vote = np.argmax( output )
votes.append(vote)
return np.asarray( votes )
def calc_accuracy(votes, answers):
return np.sum(votes == answers)/float(len(votes))
def find_initial_nn_classifier(
dataset, correct_answers,
architecture, activation_functions = (np.tanh,),
find_promising_initial_nn_max_tries = 100):
""" The architecture specifies the number of inputs and outputs
of each layer (and thus the layer sizes). The first value in the
architecture list should be the numberof features in the dataset
and the last the number of classes.
It is required that the neural network is *promising*, that is,
it is balanced enough to generate all labels. If generating such
promising NN fails, None is returned."""
for tryc in range(find_promising_initial_nn_max_tries):
# Create a NN
all_layers = []
for l_idx in range(1,len(architecture)):
l_in = architecture[l_idx-1]
l_out = architecture[l_idx]
l_act = activation_functions[-1]
if l_idx<len(activation_functions):
l_act = activation_functions[l_idx]
# Weights are random values on a range [-1.0,1.0]
# +1 is the bias
layer = Layer(np.random.rand(l_out, l_in+1)*2-1,
l_act)
all_layers.append(layer)
# Test NN, require that it outputs every class at least once
votes = nn_votes( all_layers, dataset )
if len(set(votes))==nclasses:
print( "Found promising initial solution on try %d, with accuracy %.2f"%\
(tryc, calc_accuracy(votes, correct_answers)) )
return all_layers
print( "WARNING: Failed to find a promising initial solution!" )
return None # failed
Machine learning is all about fitting the model to the data. Neural network is just another model, which can be thought as a function
The canonical way of doing this would be Backpropagation, which is not too hard to reason about, but involves some calculus in addition to linear algebra.
In this exercise we use Differential Evolution (DE), which is conceptually simpler and perhaps more interesting from the machine learning perspective. It is a population based iterative generic optimization method. Each iteration of DE consists of
*Image source: Mahdavi et al (2017) Analyzing Effects of...*
from random import random, sample
Best = namedtuple('Best', 'value index agent')
def differential_evolution(
# domain
agent_fitness, init_agent, agent_to_vec, vec_to_new_agent,
# settings
iterations=100, NP=25, CR=0.8, F=0.5):
""" This maximizes the objective for a population of agents
with differential evolution. It takes following parameters:
iterations -- number of improvement iterations (default 100)
NP -- the population size (default 25)
CR -- vector value crossover pobability (default 0.8)
F -- differential weight (default 0.5)
The opimization domain is specified with callbacks:
agent_fitness(agent) -> float
init_agent() -> agent
agent_to_vec(agent) -> ndarray(1d)
vec_to_new_agent(ndarray(1d), old_agent) -> new_agent
"""
# init population
best = Best(0.0, -1, None)
population = []
obj_f_vals = []
for i in range(NP):
agent = init_agent()
if agent!=None:
population.append(agent)
obj_f = agent_fitness(agent)
obj_f_vals.append(obj_f)
if obj_f>best.value:
best = Best(obj_f, len(population)-1, agent)
nagents = len(population)
print( "Initialized a population of size %d"%nagents )
abc_indices = range( nagents-1 )
for iterc in range(iterations):
improvements = 0
for i in range(len(population)):
agent_x = population[i]
objf_x = obj_f_vals[i]
sel_abc = [(j if j<i else j+1)
for j in sample(abc_indices, 3)]
agent_a, agent_b, agent_c = \
[population[j] for j in sel_abc]
vec_x = agent_to_vec(agent_x)
vec_a = agent_to_vec(agent_a)
vec_b = agent_to_vec(agent_b)
vec_c = agent_to_vec(agent_c)
# New trial solution
vec_xt = vec_x.copy()
cr_mask = np.random.rand(len(vec_xt))<CR
vec_xt[cr_mask] = vec_a[cr_mask]+\
F*(vec_b[cr_mask]-vec_c[cr_mask] )
# Evaluate the trial
agent_xt = vec_to_new_agent(vec_xt, agent_x)
objf_xt = agent_fitness(agent_xt)
# Maximize (replace if better accuracy)
if objf_xt>objf_x:
population[i] = agent_xt
obj_f_vals[i] = objf_xt
improvements+=1
if objf_xt>best.value:
best = Best(objf_xt, i, agent_xt)
print( "DE Iteration %d: improved %d/%d agents (best %.2f)"%\
(iterc, improvements, nagents, best.value) )
return bestNow it is time to specify the functions that are needed to train the neural network using DE. We use a neural network with an architecture of 4 input neurons (one for each feature), 3 output neurons (one for each class) and two hidden layers with 8 and 5 neurons. Why 8 and 5 you ask? That is why machine learning is sometimes considered to be more art than science. The achitecture of our network is illustrated below.
def print_agent(agent):
for li, layer in enumerate(agent):
print( "layer%d#"%li,\
"wts :",layer.weights.shape,\
"af :", layer[1].__name__ )
def init_nn_agent():
architecture = (ninputs, 8, 5, nclasses) # 3 layers
return find_initial_nn_classifier(
training_dataset,
training_answers,
architecture)
def nn_agent_to_vec(agent):
return np.concatenate([np.ravel(layer.weights)
for layer in agent])
def new_nn_agent_from_vec(vec, old_agent):
from_idx = 0
to_idx = 0
new_layers = []
for layer in old_agent:
to_idx = from_idx+np.prod( layer.weights.size )
new_weights = vec[from_idx:to_idx].copy()
new_weights.shape = layer.weights.shape
new_layers.append( Layer(new_weights, layer.act_fun) )
from_idx = to_idx
return new_layers
def nn_agent_objf(agent):
votes = nn_votes(agent, training_dataset)
return calc_accuracy(votes, training_answers)
# Optimize with DE
best_nn = differential_evolution(
nn_agent_objf, init_nn_agent,
nn_agent_to_vec, new_nn_agent_from_vec,
iterations=100, NP=25, CR=0.8, F=0.5)Found promising initial solution on try 14, with accuracy 0.43
Found promising initial solution on try 7, with accuracy 0.48
Found promising initial solution on try 12, with accuracy 0.35
Found promising initial solution on try 12, with accuracy 0.32
Found promising initial solution on try 3, with accuracy 0.00
Found promising initial solution on try 4, with accuracy 0.61
Found promising initial solution on try 38, with accuracy 0.44
Found promising initial solution on try 24, with accuracy 0.00
Found promising initial solution on try 14, with accuracy 0.61
Found promising initial solution on try 15, with accuracy 0.61
Found promising initial solution on try 36, with accuracy 0.15
Found promising initial solution on try 33, with accuracy 0.36
Found promising initial solution on try 5, with accuracy 0.00
Found promising initial solution on try 52, with accuracy 0.64
Found promising initial solution on try 3, with accuracy 0.00
Found promising initial solution on try 48, with accuracy 0.61
Found promising initial solution on try 9, with accuracy 0.56
Found promising initial solution on try 53, with accuracy 0.57
Found promising initial solution on try 7, with accuracy 0.01
Found promising initial solution on try 11, with accuracy 0.39
Found promising initial solution on try 31, with accuracy 0.11
Found promising initial solution on try 3, with accuracy 0.39
Found promising initial solution on try 63, with accuracy 0.56
Found promising initial solution on try 92, with accuracy 0.65
Found promising initial solution on try 90, with accuracy 0.55
Initialized a population of size 25
DE Iteration 0: improved 10/25 agents (best 0.72)
DE Iteration 1: improved 4/25 agents (best 0.75)
DE Iteration 2: improved 4/25 agents (best 0.75)
DE Iteration 3: improved 5/25 agents (best 0.75)
DE Iteration 4: improved 4/25 agents (best 0.75)
DE Iteration 5: improved 2/25 agents (best 0.75)
DE Iteration 6: improved 3/25 agents (best 0.75)
DE Iteration 7: improved 0/25 agents (best 0.75)
DE Iteration 8: improved 1/25 agents (best 0.75)
DE Iteration 9: improved 0/25 agents (best 0.75)
DE Iteration 10: improved 1/25 agents (best 0.75)
DE Iteration 11: improved 0/25 agents (best 0.75)
DE Iteration 12: improved 0/25 agents (best 0.75)
DE Iteration 13: improved 3/25 agents (best 0.75)
DE Iteration 14: improved 1/25 agents (best 0.75)
DE Iteration 15: improved 0/25 agents (best 0.75)
DE Iteration 16: improved 0/25 agents (best 0.75)
DE Iteration 17: improved 1/25 agents (best 0.75)
DE Iteration 18: improved 0/25 agents (best 0.75)
DE Iteration 19: improved 2/25 agents (best 0.75)
DE Iteration 20: improved 0/25 agents (best 0.75)
DE Iteration 21: improved 2/25 agents (best 0.96)
DE Iteration 22: improved 0/25 agents (best 0.96)
DE Iteration 23: improved 2/25 agents (best 0.96)
DE Iteration 24: improved 1/25 agents (best 0.96)
DE Iteration 25: improved 0/25 agents (best 0.96)
DE Iteration 26: improved 1/25 agents (best 0.96)
DE Iteration 27: improved 0/25 agents (best 0.96)
DE Iteration 28: improved 0/25 agents (best 0.96)
DE Iteration 29: improved 0/25 agents (best 0.96)
DE Iteration 30: improved 0/25 agents (best 0.96)
DE Iteration 31: improved 0/25 agents (best 0.96)
DE Iteration 32: improved 0/25 agents (best 0.96)
DE Iteration 33: improved 0/25 agents (best 0.96)
DE Iteration 34: improved 0/25 agents (best 0.96)
DE Iteration 35: improved 0/25 agents (best 0.96)
DE Iteration 36: improved 1/25 agents (best 0.96)
DE Iteration 37: improved 0/25 agents (best 0.96)
DE Iteration 38: improved 0/25 agents (best 0.96)
DE Iteration 39: improved 0/25 agents (best 0.96)
DE Iteration 40: improved 1/25 agents (best 0.96)
DE Iteration 41: improved 0/25 agents (best 0.96)
DE Iteration 42: improved 0/25 agents (best 0.96)
DE Iteration 43: improved 0/25 agents (best 0.96)
DE Iteration 44: improved 1/25 agents (best 0.96)
DE Iteration 45: improved 0/25 agents (best 0.96)
DE Iteration 46: improved 0/25 agents (best 0.96)
DE Iteration 47: improved 0/25 agents (best 0.96)
DE Iteration 48: improved 0/25 agents (best 0.96)
DE Iteration 49: improved 0/25 agents (best 0.96)
DE Iteration 50: improved 1/25 agents (best 0.96)
DE Iteration 51: improved 0/25 agents (best 0.96)
DE Iteration 52: improved 0/25 agents (best 0.96)
DE Iteration 53: improved 0/25 agents (best 0.96)
DE Iteration 54: improved 0/25 agents (best 0.96)
DE Iteration 55: improved 0/25 agents (best 0.96)
DE Iteration 56: improved 0/25 agents (best 0.96)
DE Iteration 57: improved 0/25 agents (best 0.96)
DE Iteration 58: improved 0/25 agents (best 0.96)
DE Iteration 59: improved 1/25 agents (best 0.96)
DE Iteration 60: improved 0/25 agents (best 0.96)
DE Iteration 61: improved 0/25 agents (best 0.96)
DE Iteration 62: improved 0/25 agents (best 0.96)
DE Iteration 63: improved 0/25 agents (best 0.96)
DE Iteration 64: improved 0/25 agents (best 0.96)
DE Iteration 65: improved 0/25 agents (best 0.96)
DE Iteration 66: improved 0/25 agents (best 0.96)
DE Iteration 67: improved 0/25 agents (best 0.96)
DE Iteration 68: improved 0/25 agents (best 0.96)
DE Iteration 69: improved 0/25 agents (best 0.96)
DE Iteration 70: improved 0/25 agents (best 0.96)
DE Iteration 71: improved 0/25 agents (best 0.96)
DE Iteration 72: improved 0/25 agents (best 0.96)
DE Iteration 73: improved 0/25 agents (best 0.96)
DE Iteration 74: improved 0/25 agents (best 0.96)
DE Iteration 75: improved 0/25 agents (best 0.96)
DE Iteration 76: improved 0/25 agents (best 0.96)
DE Iteration 77: improved 0/25 agents (best 0.96)
DE Iteration 78: improved 0/25 agents (best 0.96)
DE Iteration 79: improved 0/25 agents (best 0.96)
DE Iteration 80: improved 0/25 agents (best 0.96)
DE Iteration 81: improved 0/25 agents (best 0.96)
DE Iteration 82: improved 0/25 agents (best 0.96)
DE Iteration 83: improved 1/25 agents (best 0.96)
DE Iteration 84: improved 0/25 agents (best 0.96)
DE Iteration 85: improved 0/25 agents (best 0.96)
DE Iteration 86: improved 0/25 agents (best 0.96)
DE Iteration 87: improved 0/25 agents (best 0.96)
DE Iteration 88: improved 0/25 agents (best 0.96)
DE Iteration 89: improved 1/25 agents (best 0.96)
DE Iteration 90: improved 0/25 agents (best 0.96)
DE Iteration 91: improved 0/25 agents (best 0.96)
DE Iteration 92: improved 0/25 agents (best 0.96)
DE Iteration 93: improved 0/25 agents (best 0.96)
DE Iteration 94: improved 0/25 agents (best 0.96)
DE Iteration 95: improved 0/25 agents (best 0.96)
DE Iteration 96: improved 0/25 agents (best 0.96)
DE Iteration 97: improved 0/25 agents (best 0.96)
DE Iteration 98: improved 0/25 agents (best 0.96)
DE Iteration 99: improved 0/25 agents (best 0.96)
Finally, it is the time to test our model. The performance on the training data is unreliable, as there might be overfitting. That is, the model works great on the training data but its performance does not generalize.
Now, test the best agent in the final DE population with the testing data that we put aside few cells back.
votes = nn_votes(best_nn.agent, testing_dataset)
print( "accuracy on testing set %.2f"%\
calc_accuracy(votes, testing_answers) )accuracy on testing set 0.89
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def ReLU(x):
return np.log(1+np.exp(x))
def softmax(x):
return np.exp(x)/np.sum(np.exp(x))